题目内容
已知集合P={(x,y)|xy=3,x>0},在映射f:P→Q的作用下,点(x,y)的像为(log3x,log3y),而Q恰为像的集合.则Q为
- A.{(x,y)|x+y=0}
- B.{(x,y)|x+y=0,x>0}
- C.{(x,y)|x+y=1}
- D.{(x,y)|x+y=1,x>0}
C
分析:根据题意,点(x,y)的象为(log3x,log3y),分析A中元素的象的性质有log3x+log3y=log3xy=1,进而分析B的元素,可得答案.
解答:根据题意,映射f:A→B在f作用下,点(x,y)的象为(log3x,log3y),
而A={(x,y)|xy=3,x>0},则其象有log3x+log3y=log3xy=1,成立;
则B中的元素(x,y),有x+y=1成立;
故B为{(x,y)|x+y=1}.
故选C.
点评:本题考查映射的应用,涉及指数的运算性质,注意从映射的定义着手分析,这是解题的关键.
分析:根据题意,点(x,y)的象为(log3x,log3y),分析A中元素的象的性质有log3x+log3y=log3xy=1,进而分析B的元素,可得答案.
解答:根据题意,映射f:A→B在f作用下,点(x,y)的象为(log3x,log3y),
而A={(x,y)|xy=3,x>0},则其象有log3x+log3y=log3xy=1,成立;
则B中的元素(x,y),有x+y=1成立;
故B为{(x,y)|x+y=1}.
故选C.
点评:本题考查映射的应用,涉及指数的运算性质,注意从映射的定义着手分析,这是解题的关键.

练习册系列答案
相关题目
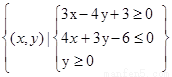 ,Q={(x,y)|(x-a)2+(y-b)2≤r2(r>0), 若“点M∈P”是“点M∈Q”的必要条件,则当r最大时ab的值是_____
,Q={(x,y)|(x-a)2+(y-b)2≤r2(r>0), 若“点M∈P”是“点M∈Q”的必要条件,则当r最大时ab的值是_____