题目内容
已知函数f(x)=ln(1+x2)+ax(a≤0),
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明: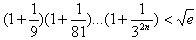 (n∈N*,e为自然对数的底数)。
(n∈N*,e为自然对数的底数)。
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明:
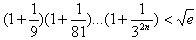 (n∈N*,e为自然对数的底数)。
(n∈N*,e为自然对数的底数)。 解:(1) ,
,
∵x=0是f(x)的一个极值点,
则 ,
,
∴a=0,验证知a=0符合条件;
(2) ,
,
1)若a=0时,
∴f(x)在 上单调递增,在(-∞,0)单调递减;
上单调递增,在(-∞,0)单调递减;
2)若 ,得当a≤-1时,
,得当a≤-1时, 对x∈R恒成立,
对x∈R恒成立,
∴f(x)在R上单调递减;
3)若-1<a<0时,由 ,
,
∴ ,
,
再令 ,可得
,可得 ,
,
∴ 上单调递增,
上单调递增,
在 上单调递减;
上单调递减;
综上所述,若a≤-1时,f(x)在 上单调递减;
上单调递减;
若-1<a<0时, 上单调递增,
上单调递增,
在 上单调递减;
上单调递减;
若a=0时,f(x)在 上单调递增,在(-∞,0)单调递减。
上单调递增,在(-∞,0)单调递减。
(3)由(2)知,当a=-1时,f(x)在 上单调递减,
上单调递减,
当x∈ 时,由
时,由 ,
,
∴ ,
,
∴
 ,
,
∴ 。
。
 ,
,∵x=0是f(x)的一个极值点,
则
 ,
,∴a=0,验证知a=0符合条件;
(2)
 ,
,1)若a=0时,
∴f(x)在
 上单调递增,在(-∞,0)单调递减;
上单调递增,在(-∞,0)单调递减;2)若
 ,得当a≤-1时,
,得当a≤-1时, 对x∈R恒成立,
对x∈R恒成立,∴f(x)在R上单调递减;
3)若-1<a<0时,由
 ,
,∴
 ,
,再令
 ,可得
,可得 ,
,∴
 上单调递增,
上单调递增,在
 上单调递减;
上单调递减;综上所述,若a≤-1时,f(x)在
 上单调递减;
上单调递减;若-1<a<0时,
 上单调递增,
上单调递增,在
 上单调递减;
上单调递减;若a=0时,f(x)在
 上单调递增,在(-∞,0)单调递减。
上单调递增,在(-∞,0)单调递减。(3)由(2)知,当a=-1时,f(x)在
 上单调递减,
上单调递减,当x∈
 时,由
时,由 ,
,∴
 ,
,∴

 ,
,∴
 。
。
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目