题目内容
已知a>0,b>0,2a+b=16,则ab的最大值为 .
【答案】分析:由a>0,b>0,2a+b=16,可得ab=a(16-2a),利用基本不等式可求得ab的最大值.
解答:解:∵a>0,b>0,2a+b=16,∴ab=a(16-2a)= •2a(16-2a)≤
•2a(16-2a)≤ •
•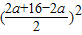 =32(当且仅当a=4时取“=”).
=32(当且仅当a=4时取“=”).
故答案为:32.
点评:本题考查基本不等式,着重考查学生对基本不等式“a>0,b>0,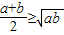 ”的变形“a>0,b>0,
”的变形“a>0,b>0,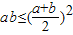 ”的灵活运用,属于中档题.
”的灵活运用,属于中档题.
解答:解:∵a>0,b>0,2a+b=16,∴ab=a(16-2a)=
 •2a(16-2a)≤
•2a(16-2a)≤ •
•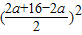 =32(当且仅当a=4时取“=”).
=32(当且仅当a=4时取“=”).故答案为:32.
点评:本题考查基本不等式,着重考查学生对基本不等式“a>0,b>0,
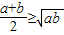 ”的变形“a>0,b>0,
”的变形“a>0,b>0,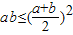 ”的灵活运用,属于中档题.
”的灵活运用,属于中档题. 
练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目