题目内容
等差数列{an}中,公差d≠0,a2是a1与a4的等比中项,已知数列a1,a3,ak , ak
, ak ,…, ak
,…, ak ,…成等比数列.
,…成等比数列.
(1)求数列{kn}的通项kn;
(2)求数列 的前n项和Sn.
的前n项和Sn.
 , ak
, ak ,…, ak
,…, ak ,…成等比数列.
,…成等比数列.(1)求数列{kn}的通项kn;
(2)求数列
 的前n项和Sn.
的前n项和Sn.(1)kn1=3n+1(2)Sn=
 -
-

 -
-
(1)由已知得(a1+d)2=a1·(a1+3d),解得a1=d或d=0(舍去),所以数列{an}的通项是an=nd,因为数列a1,a3,ak ,ak
,ak ,…,ak
,…,ak ,…成等比数列,即数列d,3d,k1d,k2d,…,knd,…成等比数列,其公比q=
,…成等比数列,即数列d,3d,k1d,k2d,…,knd,…成等比数列,其公比q= =3,k1d=32d,故k1=9,所以数列{kn}是以k1=9为首项,以3为公比的等比数列,故kn=9×3n-1=3n+1.
=3,k1d=32d,故k1=9,所以数列{kn}是以k1=9为首项,以3为公比的等比数列,故kn=9×3n-1=3n+1.
(2)Sn= +
+ +
+ +…+
+…+ ①
①
 Sn=
Sn= +
+ +
+ +…+
+…+ +
+ ②
②
①-②并整理得Sn=
 -
- .
.
 ,ak
,ak ,…,ak
,…,ak ,…成等比数列,即数列d,3d,k1d,k2d,…,knd,…成等比数列,其公比q=
,…成等比数列,即数列d,3d,k1d,k2d,…,knd,…成等比数列,其公比q= =3,k1d=32d,故k1=9,所以数列{kn}是以k1=9为首项,以3为公比的等比数列,故kn=9×3n-1=3n+1.
=3,k1d=32d,故k1=9,所以数列{kn}是以k1=9为首项,以3为公比的等比数列,故kn=9×3n-1=3n+1.(2)Sn=
 +
+ +
+ +…+
+…+ ①
① Sn=
Sn= +
+ +
+ +…+
+…+ +
+ ②
② ①-②并整理得Sn=

 -
- .
.
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 满足条件:
满足条件: ,且
,且 )
)
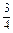 x·sin
x·sin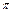 )·sin
)·sin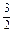 (x+3
(x+3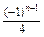 (n=1,2,3,…).
(n=1,2,3,…).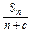 ,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.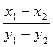 =____________.
=____________.