Question

直三棱柱ABC-A₁B₁C₁中，AB⊥BC，E是A₁C的中点，ED⊥A₁C且交AC于D，A₁A=AB=BC；

(Ⅰ)证明：B₁C₁∥平面A₁BC；

(Ⅱ)求平面A₁AB与平面EDB所成的二面角的大小；(仅考虑平面角为锐角的情况)；

(Ⅲ)在线段A₁C上是否存在点M，使得几何体B-ADMA₁与三棱锥C—ABA₁的体积之比为2：3，若存在，请确定点M的位置；若不存在，请说明理由．

Answer 1

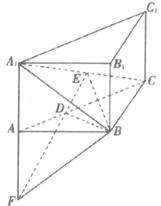
(Ⅰ)证：在三棱柱ABC-A₁B₁C₁中，

∵B₁C₁∥BC，又BE平面A₁BC，

∴B₁C₁∥平面A₁BC.

(Ⅱ)∵A₁A、ED平面A₁AC，且A₁A、ED不平行．

故延长A₁A、ED后必相交，设交点为9，连接FB

∴A₁-FB-E是所求二面角；依条件易证明

Rt△A₁EF≌Rt△A₁AC．  ∵E为A₁C中点，

∴A为A₁F中点    ∴AF=A₁A=AB，

∠A₁BA=∠ABF=45°，∠A₁BF=90°．

即A₁B⊥FB．又A₁E⊥平面EFB，∴EB⊥FB

∴∠A₁BE是所求的二面角的平面角．

∵E是等腰直角三角形A₁BC底边中点，

∴∠A₁BE=45°．故所求的二面角的大小为45°

(Ⅲ)据题知AA₁=AB=BC，

∴AC=AA₁，设AA₁=a，则有AA₁=AB=a，

BC=a，AC=a，A₁C=,

由△CED∽△CAA₁，

∴,

设M到面ABC的距离为h，

据题意知，h即为M到AC的距离，

∴,

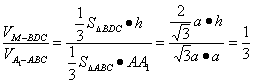∴h=， ∴CM=A₁C，即M在A₁C的中点时有=2：3