题目内容
4.一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:| 人数xi(人) | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 件数yi(件) | 4 | 7 | 12 | 12 | 20 | 23 | 27 |
参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x\overline{y}}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$
(1)由散点图可知进店人数和商品销售件数成线性相关关系,设回归方程为$\widehat{y}$=bx+a,求该回归方程(b保留到小数点后两位);
(2)预测进店80人时,商品销售的件数(结果保留整数).
分析 (1)根据所给的数据,做出x,y的平均数,即得到这组数据的样本中心点,根据最小二乘法做出线性回归方程的系数,写出线性回归方程.
(2)利用上一问做出的线性回归方程,把x的值代入方程,预报出对应的y的值
解答 解:(1).∵$\sum_{i=1}^{7}$xiyi=3245,$\overline{x}$=25,$\overline{y}$≈15,$\sum_{i=1}^{7}$xi2=5075,
∴b=$\frac{\sum _{i=1}^{7}{x}_{i}{y}_{i}-7\overline{x}\overline{y}}{\sum _{i=1}^{7}{x}_{i}^{2}-7{\overline{x}}^{2}}$=$\frac{3245-7×25×15}{5075-7×{25}^{2}}$≈0.89,…(6分)
a=$\overline{y}$-b$\overline{x}$=-7.25…(8分)
∴回归直线方程是y=0.89x-7.25…(9分)
(2)进店人数80人时,商品销售的件数$\hat{y}$=0.89×80-7.25≈64件,
即进店80人时,商品销售的件数约为64件.
点评 本题考查线性回归方程,考查最小二乘法求线性回归方程的系数,考查样本中心点的求法,本题的运算量比较大,是一个综合题目

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若M点的极坐标为$({2,\frac{5π}{6}})$,则M点的直角坐标是( )
| A. | (-$\sqrt{3}$,1) | B. | (-$\sqrt{3}$,-1) | C. | ($\sqrt{3}$,-1) | D. | ($\sqrt{3}$,1) |
19.设函数f(x)是定义在R上的奇函数,且对任意x∈R都有f(x)=f(x+4),当x∈(0,2)时,f(x)=2x,则f(2015)+f(2012)的值为( )
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
9.如图程序图输出的结果是( )
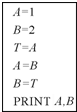
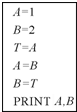
| A. | 2,1 | B. | 2,2 | C. | 1,2 | D. | 1,1 |
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB.