题目内容
设O、A、B、C为平面内四点,| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| c |
分析:欲求|
|2+|
|2+|
|2,根据向量的性质知,只须求出(
)2+(
)2+(
)2,结合条件,只须将式子
+
+
=
平方即得.
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
解答:解:∵
+
+
=
,平方得:
|
|2+|
|2+|
|2+2(
•
+
•
+
•
)=0,
∵
•
=
•
=
•
=-1
∴|
|2+|
|2+|
|2+2×(-3)=0,
∴|
|2+|
|2+|
|2=6
故答案为:6.
| a |
| b |
| c |
| 0 |
|
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
∵
| a |
| b |
| b |
| c |
| c |
| a |
∴|
| a |
| b |
| c |
∴|
| a |
| b |
| c |
故答案为:6.
点评:本小题主要考查向量的模的应用、向量的数量积的应用等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )
3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( ) 是实数,则正整数n的最小值是4
是实数,则正整数n的最小值是4 ∈
∈
 都是非零复数,
都是非零复数,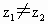 ,且复平面上O为原点,点A和B分别与
,且复平面上O为原点,点A和B分别与 和
和 对应,∠AOB=
对应,∠AOB= ,则
,则
 |≤1,则
|≤1,则 ≤arg(-zi)≤
≤arg(-zi)≤ ,其中真命题是
,其中真命题是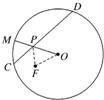 如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是
如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是