题目内容
对于函数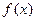 ,若存在
,若存在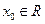 ,使
,使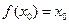 成立,则称
成立,则称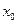 为
为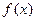 的不动点。如果
的不动点。如果
函数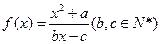 有且仅有两个不动点
有且仅有两个不动点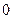 、
、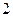 ,且
,且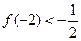 。
。
(1)试求函数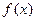 的单调区间;
的单调区间;
(2)点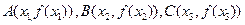 从左到右依次是函数
从左到右依次是函数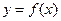 图象上三点,其中
图象上三点,其中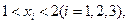 求证:⊿
求证:⊿ 是钝角三角形.
是钝角三角形.
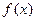 ,若存在
,若存在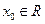 ,使
,使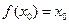 成立,则称
成立,则称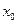 为
为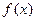 的不动点。如果
的不动点。如果函数
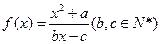 有且仅有两个不动点
有且仅有两个不动点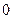 、
、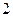 ,且
,且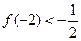 。
。(1)试求函数
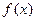 的单调区间;
的单调区间;(2)点
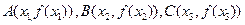 从左到右依次是函数
从左到右依次是函数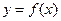 图象上三点,其中
图象上三点,其中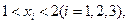 求证:⊿
求证:⊿ 是钝角三角形.
是钝角三角形.函数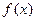 的单调递增区间为
的单调递增区间为 和
和 ,单调减区间为
,单调减区间为 和
和
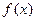 的单调递增区间为
的单调递增区间为 和
和 ,单调减区间为
,单调减区间为 和
和
(1)设
 ∴
∴ ∴
∴ 由
由 又∵
又∵ ∴
∴
∴ 于是
于是
由 得
得 或
或 ; 由
; 由 得
得 或
或
故函数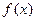 的单调递增区间为
的单调递增区间为 和
和 ,单调减区间为
,单调减区间为 和
和
(2)证明:据题意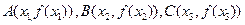 且x1<x2<x3,
且x1<x2<x3,
由(1)知f (x1)>f (x2)>f (x3),


 即⊿
即⊿ 是钝角三角形.
是钝角三角形.

 ∴
∴ ∴
∴ 由
由 又∵
又∵ ∴
∴
∴
 于是
于是
由
 得
得 或
或 ; 由
; 由 得
得 或
或
故函数
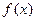 的单调递增区间为
的单调递增区间为 和
和 ,单调减区间为
,单调减区间为 和
和
(2)证明:据题意
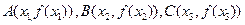 且x1<x2<x3,
且x1<x2<x3, 由(1)知f (x1)>f (x2)>f (x3),



 即⊿
即⊿ 是钝角三角形.
是钝角三角形.
练习册系列答案
相关题目
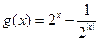 .
.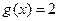 ,求
,求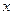 的值;
的值;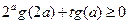 对于
对于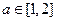 恒成立,求实数
恒成立,求实数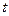 的取值范围.
的取值范围.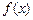 的定义域内任意的
的定义域内任意的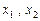 ,都有
,都有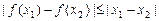 成立,那么就称函数
成立,那么就称函数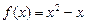 ,
,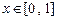 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数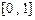 上的“平缓函数”,且
上的“平缓函数”,且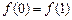 .证明:对于任意的
.证明:对于任意的
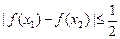 成立.(3)设
成立.(3)设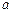 、
、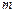 为实常数,
为实常数,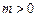 .若
.若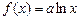 是区间
是区间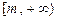 上的“平缓函数”,试估计
上的“平缓函数”,试估计 在
在 上递减,那么
上递减,那么 在
在 上( )
上( ) 递增且无最大值 B
递增且无最大值 B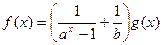 (a>0且a≠1)为偶函数,则常数b的值为( )
(a>0且a≠1)为偶函数,则常数b的值为( )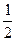
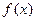 的定义域为R,若存在常数
的定义域为R,若存在常数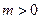 ,使
,使 对一切实数
对一切实数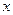 均成立,则称
均成立,则称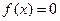 ;②
;②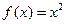 ;③
;③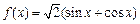 ;④
;④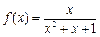 ;⑤
;⑤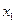 ,
,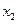 均有
均有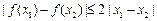 .其中是“倍约束函数”的序号是
.其中是“倍约束函数”的序号是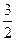 ,-
,-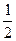 )
)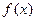 是定义在R上的偶函数,且
是定义在R上的偶函数,且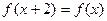 ,当0≤
,当0≤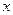 ≤1时,
≤1时,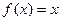 ,则当5≤
,则当5≤