Question

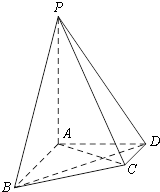（2013•成都模拟）在四棱锥P-ABCD中，AB∥CD，AB⊥AD，AB=4，AD=2

2

，CD=2，PA⊥平面ABCD，PA=4．
（Ⅰ）设平面PAB∩平面PCD=m，求证：CD∥m；
（Ⅱ）求证：BD⊥平面PAC；
（Ⅲ）设点Q为线段PB上一点，且直线QC与平面PAC所成角的正弦值为

3

3

，求

PQ

PB

的值．

Answer 1

分析：（Ⅰ）利用平行四边形的性质和平行线的传递性即可找出两个平面的交线并且证明结论；
（Ⅱ）利用已知条件先证明BD⊥AC，再利用线面垂直的性质定理和判定定理即可证明；
（Ⅲ）通过结论空间直角坐标系，利用法向量与斜线所成的角即可找出Q点的位置．

解答：解：（Ⅰ）如图所示，过点B作BM∥PA，并且取BM=PA，连接PM，CM．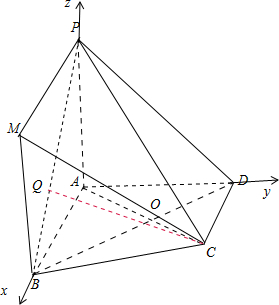
∴四边形PABM为平行四边形，∴PM∥AB，
∵AB∥CD，∴PM∥CD，即PM为平面PAB∩平面PCD=m，m∥CD．
（Ⅱ）在Rt△BAD和Rt△ADC中，由勾股定理可得
BD=

42+(2 2 )2

=2

6

，AC=

22+(2 2 )2

=2

3

．
∵AB∥DC，∴

OD

OB

=

OC

OA

=

2

4

=

1

2

，
∴OD=

1

3

BD=

2 6

3

，OC=

1

3

AC=

2 3

3

．
∴OD²+OC²=(

2 6

3

)2+(

2 3

3

)2=4=CD²，
∴OC⊥OD，即BD⊥AC；
∵PA⊥底面ABCD，∴PA⊥BD．
∵PA∩AC=A，∴BD⊥平面PAC．
（Ⅲ）建立如图所示的空间直角坐标系，则A（0，0，0），
B（4，0，0），D（0，2

2

，0），C（2，2

2

，0），P（0，0，4）．
∴

PB

=(4，0，-4)，
设

PQ

=λ

PB

，则Q（4λ，0，4-4λ），∴

QC

=(2-4λ，2

2

，4λ-4)．

BD

=(-4，2

2

，0)，由（2）可知

BD

为平面PAC的法向量．
∴cos＜

BD

，

QC

＞=

BD • QC

| BD | | QC |

=

16λ

2 6 (2-4λ)2+(2 2 )2+(4λ-4)2

，
∵直线QC与平面PAC所成角的正弦值为

3

3

，
∴

3

3

=

|16λ|

2 6 (2-4λ)2+8+(4λ-4)2

，
化为12λ=7，解得λ=

7

12

．
∴

PQ

PB

=

7

12

．

点评：熟练掌握平行四边形的性质、平行线的传递性、线面垂直的性质定理和判定定理及法向量与斜线所成的角是解题的关键．