题目内容
已知平面直角坐标系 ,以
,以 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, 点的极坐标为
点的极坐标为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为
(1)写出点 的直角坐标及曲线
的直角坐标及曲线 的直角坐标方程;
的直角坐标方程;
(2)若 为曲线
为曲线 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
( 为参数)距离的最小值.
为参数)距离的最小值.
(1)点 的直角坐标
的直角坐标 ,曲线
,曲线 的直角坐标方程为
的直角坐标方程为 ;(2)点
;(2)点 到直线
到直线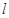 的最小距离为
的最小距离为 .
.
解析试题分析:本题考查极坐标和直角坐标的互化,参数方程和普通方程的互化,考查学生的转化能力和计算能力.第一问,利用极坐标与直角坐标的互化公式得出 点的直角坐标和曲线
点的直角坐标和曲线 的方程;第二问,先把曲线
的方程;第二问,先把曲线 的直角坐标方程化为参数方程,得到
的直角坐标方程化为参数方程,得到 点坐标,根据点到直线的距离公式列出表达式,根据三角函数的值域求距离的最小值.
点坐标,根据点到直线的距离公式列出表达式,根据三角函数的值域求距离的最小值.
试题解析:(1) 点 的直角坐标
的直角坐标
由 得
得 ,即
,即
所以曲线 的直角坐标方程为
的直角坐标方程为 4分
4分
(2)曲线 的参数方程为
的参数方程为 (
(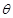 为参数)直线
为参数)直线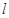 的普通方程为
的普通方程为
设 ,则
,则 .那么点
.那么点 到直线
到直线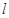 的距离[
的距离[ .
. ,所以点
,所以点 到直线
到直线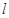 的最小距离为
的最小距离为 10分
10分
考点:1.极坐标与直角坐标的互化;2.参数方程与普通方程的互化;3.点到直线的距离公式.

练习册系列答案
相关题目
 中,圆的参数方程为
中,圆的参数方程为 ,以坐标原点
,以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.求:
轴的正半轴为极轴建立极坐标系.求: ,圆心为直线ρsin
,圆心为直线ρsin =-
=- 与极轴的交点,求圆C的极坐标方程.
与极轴的交点,求圆C的极坐标方程.
 (t为参数)和圆C的极坐标方程:ρ=2
(t为参数)和圆C的极坐标方程:ρ=2 sin(θ+
sin(θ+ ).
). (
( 为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点
为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点 ,直线
,直线 的极坐标方程为
的极坐标方程为 .
. 与直线
与直线 的值.
的值. ,直线
,直线 的参数方程为
的参数方程为 ( t为参数,0≤
( t为参数,0≤ <
< ).
). 的参数方程是
的参数方程是 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在 .
. 的取值范围.
的取值范围. (为参数),曲线C的极坐标方程为
(为参数),曲线C的极坐标方程为 .
. 中,曲线
中,曲线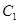 为
为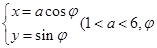 为参数)。在以
为参数)。在以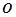 为原点,
为原点,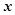 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线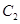 的极坐标方程为
的极坐标方程为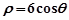 ,射线为
,射线为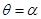 ,与
,与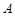 ,与
,与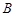 。当
。当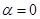 时,
时,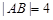 。
。 轴正半轴交点为
轴正半轴交点为 ,当
,当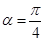 时,设直线
时,设直线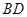 与曲线
与曲线 ,求
,求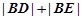 。
。