题目内容
对于函数
，若
为某一三角形的三边长，则称为“可构造三角形函数”．已知函数
是“可构造三角形函数”，则实数t的取值范围是（ ）
A． | B． | C． | D． |
D．
解析试题分析：由已知得
．
当
时，
，由
，得
；当
时，
显然是“可构造三角形函数”；当
时，
，则
．综上所述：
，故选D．
考点：函数的性质（有界性、最大值和最小值）．
练习册系列答案
相关题目
由表格中的数据可以判定方程
的一个零点所在的区间是
，则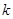
的值为（ ）
 | -1 | 0 | 1 | 2 | 3 |
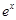 | 0．37 | 1 | 2．72 | 7．39 | 20．09 |
 | 1 | 2 | 3 | 4 | 5 |
一次函数
的图像过点
和
，则下列各点在函数的图像上的是( )
A． | B． | C． | D． |
成中心对称，且对任意的实数x都有f(x)＝－f
，f(－1)＝1，f(0)＝－2，则f(1)＋f(2)＋…＋f(2013)＝( )已知函数f(x)是R上的单调增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值( )
| A．恒为正数 | B．恒为负数 |
| C．恒为0 | D．可正可负 |
对实数a和b,定义运算“?”:a?b=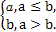
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
A．(-∞,-1)∪(- ,0) | B．{-1,-} |
| C．(-1,-) | D．(-∞,-1)∪[-,0) |
如图,虚线部分是四个象限的角平分线, 实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
| A．x2sinx | B．xsinx |
| C．x2cosx | D．xcosx |
若偶函数f(x)在(-∞,0)上单调递减,则不等式f(-1)<f(lgx)的解集是( )
| A．(0,10) | B．( ,10) |
| C．(,+∞) | D．(0,)∪(10,+∞) |
