若sin2θ=$\frac{2}{3}$.则tanθ+$\frac{1}{tanθ}$=( )A．$\sqrt{2}$B．$\sqrt{3}$C．2D．3 题目和参考答案——青夏教育精英家教网—

题目内容

18．若sin2θ=$\frac{2}{3}$，则tanθ+$\frac{1}{tanθ}$=（　　）

A．

$\sqrt{2}$

B．

$\sqrt{3}$

C．

D．

分析已知等式左边利用二倍角的正弦函数公式化简求出sinθcosθ的值，原式利用同角三角函数间基本关系化简后，将sinθcosθ的值代入计算即可求出值．

解答解：∵sin2θ=2sinθcosθ=$\frac{2}{3}$，即sinθcosθ=$\frac{1}{3}$，
∴原式=$\frac{sinθ}{cosθ}$+$\frac{cosθ}{sinθ}$=$\frac{si{n}^{2}θ+co{s}^{2}θ}{sinθcosθ}$=$\frac{1}{sinθcosθ}$=3，
故选：D．

点评此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．

练习册系列答案

9．设f（x）=$\frac{4^x}{{2+{4^x}}}$，记[m]表示不超过实数m的最大整数，例如[1.2]=1，[-0.5]=-1，[2]=2，则函数$y=[f（x）-\frac{1}{2}]+[f（1-x）-\frac{1}{2}]$的值域为{-1，0}．

6．将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）的图象，若g（x）的图象关于直线x=$\frac{π}{3}$对称，则φ的最小值为（　　）

13．在长方体ABCD-A₁B₁C₁D₁中，如果对角线AC₁与过点A的相邻三个面所成的角分别是α，β，γ，那么cos²α+cos²β+cos²γ=2．

3．若以直角坐标系xOy的O为极点，Ox为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程是ρ=$\frac{6cosθ}{si{n}^{2}θ}$．
（1）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；
（2）若直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{3}{2}+t}\\{y=\sqrt{3}t}\end{array}\right.$（t为参数）当直线l与曲线C相交于A，B两点，求|$\overrightarrow{AB}$|

10．

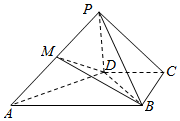在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=2，AB=4，AB∥CD，∠BCD=90°，M为棱PA的中点．
（I）证明：平面BDM⊥平面PAD；
（Ⅱ）在棱PC上是否存在一点N，使得直线BN与平面BDM所成角为30°？若存在，求出CN长，若不存在，请说明理由．

7．

执行如图所示的程序框图，则输出的n=（　　）

8．

如图表示的是求首项为-41，公差为2的等差数列前n项和的最小值的程序框图，如果?②中填a=a+2，则①?可填写a＞0．

试题分类