题目内容
已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为a的正方形，侧棱AA1的长为b，∠A1AB=∠A1AD=120°．（Ⅰ）求对角线AC1的长．
（Ⅱ）求直线BD1和AC的夹角．
分析：（Ⅰ）直接根据向量的加法把所求问题分解，再平方计算出模长的平方，进而求出结论；
（Ⅱ）先把两个向量转化，并分别求出模长以及其数量积，再代入向量的夹角计算公式即可．
（Ⅱ）先把两个向量转化，并分别求出模长以及其数量积，再代入向量的夹角计算公式即可．
解答：解：（Ⅰ）因为
=
+
+
；
∴
2=（
+
+
）2
=
2+
2+
2+2
•
+2
•
+2
•
=b2+a2+a2+2abcos120°+2abcos120°+2a•acos90°
=b2+2a2-2ab．
∴AC1=
．
（Ⅱ）∵
=
+
，
=
+
+
；
∴|
|=
=
=
=
a；
|
|=
=
=
=
．
•
=（
+
）•（
+
+
）
=
•
+
•
+
•
+
•
+
•
+
•
=ab；
∴cos＜
，
＞=
=
．
所以直线BD1和AC的夹角为：arccos
| AC1 |
| AA 1 |
| A 1B1 |
| B1C1 |
∴
| AC 1 |
| AA 1 |
| A 1B1 |
| B1C1 |
=
| AA 1 |
| A1B1 |
| B 1C1 |
| AA 1 |
| A 1B1 |
| AA 1 |
| B 1C1 |
| A 1B1 |
| B1C1 |
=b2+a2+a2+2abcos120°+2abcos120°+2a•acos90°
=b2+2a2-2ab．
∴AC1=
| b2+2a 2-2ab |
（Ⅱ）∵
| AC |
| AB |
| BC |
| D1B |
| D1A1 |
| A1B1 |
| B1B |
∴|
| AC |
(
|
|
| a2+a2+2a 2cos90° |
| 2 |
|
| D1B |
(
|
=
|
=
| a2+b2+a2+2abcos60°+2a 2cos90°+2abcos120° |
| 2a2+b2 |
| AC |
| D1B |
| AB |
| BC |
| D1A1 |
| A1B1 |
| B1B |
=
| AB |
| D1A1 |
| AB |
| A1B1 |
| AB |
| B1B |
| BC |
| D1A1 |
| BC |
| A1B1 |
| BC |
| B1B |
∴cos＜
| D1B |
| AC |
| ab | ||||
|
| b | ||
|
所以直线BD1和AC的夹角为：arccos
| b | ||
|
点评：本题主要考察异面直线所成的角以及两点间的距离计算．注意在利用向量求两直线的夹角时，要的是小于等于90度的角，避免出错．
练习册系列答案
每课必练系列答案
相关题目
如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
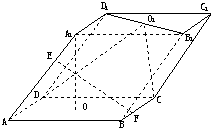如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
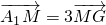，设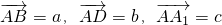
，用向量a、b、c表示向量
；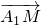