题目内容
 已知函数
已知函数![]() 在点
在点![]() 处取得极大值
处取得极大值![]() ,其导函数
,其导函数![]() 的图象经过点
的图象经过点![]() ,
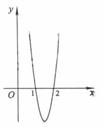
,![]() ,如图所示.求:
,如图所示.求:
(Ⅰ)![]() 的值;
的值;
(Ⅱ)![]() 的值.
的值.
解法一:
(Ⅰ)由图象可知,在(-∝,1)上![]() (x)>0,在(1,2)上
(x)>0,在(1,2)上![]() (x)<0.
(x)<0.
在(2,+∝)上![]() (x)>0.
(x)>0.
故f(x)在(-∝,1),(2,+∝)上递增,在(1,2)上递减.
因此f(x)在x=1处取得极大值,所以x0=1.
(Ⅱ) ![]() (x)=3ax2+2bx+c,
(x)=3ax2+2bx+c,
由![]() (1)=0,
(1)=0, ![]() (2)=0, f(1)=5,
(2)=0, f(1)=5,
得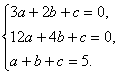 解得a=2,b=-9,c=12.
解得a=2,b=-9,c=12.
解法二:(Ⅰ)同解法一.
(Ⅱ)设![]() (x)=m(x-1)(x-2)=mx2-3mx+2m,
(x)=m(x-1)(x-2)=mx2-3mx+2m,
又![]() (x)=3ax2+2bx+c, 所以a=
(x)=3ax2+2bx+c, 所以a=![]() ,b=
,b=![]() ,c=2m
,c=2m
f(x)=![]() 由f(l)=5, 即
由f(l)=5, 即![]() 得m=6.
得m=6.
所以a=2,b=-9,c=12.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 在点
在点 处取得极小值-4,使其导数
处取得极小值-4,使其导数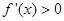 的
的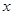 的取值范围为
的取值范围为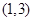 ,求:
,求: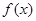 的解析式;
的解析式;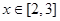 ,求
,求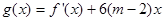 的最大值;
的最大值;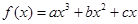 在点
在点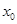 处取得极小值-4,使其导数
处取得极小值-4,使其导数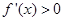 的
的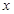 的取值范围为
的取值范围为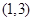 ,求:
,求: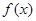 的解析式;
的解析式;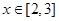 ,求
,求 的最大值;
的最大值;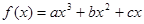 在点
在点 处取得极小值-4,使其导函数
处取得极小值-4,使其导函数 的
的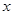 的取值范围为(1,3)
的取值范围为(1,3) 的解析式及
的解析式及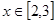 时,求
时,求 的最大值。
的最大值。