题目内容
已知双曲线x2-y2=1,点F1、F2为其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+|PF2|的值为 .
【答案】
2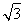
【解析】设P在双曲线右支上,|PF2|=x(x>0),
则|PF1|=2+x.
∵PF1⊥PF2,
∴(x+2)2+x2=(2c)2=8,
即:x2+2x-2=0,
解得:x=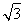-1,x+2=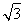+1.
∴|PF1|+|PF2|=2.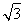
练习册系列答案
应用题作业本系列答案
相关题目
已知双曲线x2-y2=a2（a＞0）的左、右顶点分别为A、B，双曲线在第一象限的图象上有一点P，∠PAB=α，∠PBA=β，∠APB=γ，则（ ）
| A、tanα+tanβ+tanγ=0 | B、tanα+tanβ-tanγ=0 | C、tanα+tanβ+2tanγ=0 | D、tanα+tanβ-2tanγ=0 |