题目内容
判定下列命题的真假.
(1)![]() x∈R,x2+3>0;(2)
x∈R,x2+3>0;(2)![]() x∈N,x4≥1;
x∈N,x4≥1;
(3)![]() x∈Z,x3<1;(4)
x∈Z,x3<1;(4)![]() x∈Q,x2=3.
x∈Q,x2=3.
答案:
解析:
提示:
解析:
|
解:(1) ∴x2+3>0.∴命题“ (2)由于0∈N,当x=0时,x4≥1不成立, ∴命题“ (3)由于-1∈Z,当x=-1时,能使x3<1, ∴命题“ (4)由于使x2=3成立的数只有± ∴命题“ |
提示:
|
要判定一个全称命题是真命题,必须对限定集合M中的每个元素x,证明p(x)成立;判定全称命题是假命题,只要能举出集合M中的一个x=x0,使得p(x0)不成立即可,即举出一个反例就行.要判定一个存在性命题是真命题,只要在限定集合M中,至少能找到一个x=x0,使p(x0)成立即可,否则,这个存在性命题是假命题. |

练习册系列答案
相关题目
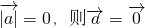 ;
;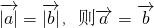 ;
;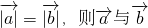 是平行向量.
是平行向量.