Question

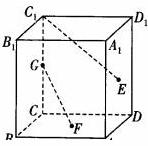
E，F，G分别为正方体ABCD-A₁B₁C₁D₁面A₁C₁，B₁C，CD₁的对角线交点，则AE与FG所成的角为

1. A.
   60⁰
2. B.
   90⁰
3. C.
   30⁰
4. D.
   45⁰

Answer 1

B
分析：由正方体的几何特征，及三角形中位线定理，可得GF∥BD，即AE与FG所成的角等于AE与BD所成的角，根据已知条件，易证明BD⊥平面A₁C，进而由线面垂直的性质得AE⊥BD，进而得到答案．
解答：连接BD，如下图所示：

∵E，F，G分别为正方体ABCD-A₁B₁C₁D₁面A₁C₁，B₁C，CD₁的对角线交点，
可得GF∥BD
∵BD⊥AC，BD⊥A₁A，A₁A∩AC=A
∴BD⊥平面A₁C
而AE?平面A₁C
∴BD⊥AE
即FG⊥AE
故选B
点评：本题考查的知识点是异面直线及其所成的角，其中根据三角形中位线定理得到GF∥BD，进而得到AE与FG所成的角等于AE与BD所成的角，是解答本题的关键．