题目内容
若P、q是方程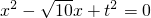 的两实根,且p,p-q,q成等比数列.
的两实根,且p,p-q,q成等比数列.
(1)求正数t的值.
(2)设 ,Sn为数列{an}的前n项和.求证:
,Sn为数列{an}的前n项和.求证: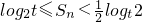 .
.
解:(1)∵P、q是方程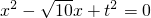 的两实根,
的两实根,
∴p+q= ,pq=t2,
,pq=t2,
∵p,p-q,q成等比数列,
∴(p-q)2=pq,即(p+q)2=5pq,
∴10=5t2,
∵t>0,∴t= .
.
(2)∵ =
= ,
,
∴Sn= =1-
=1- <1=
<1=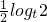 ,
,
而1- ≥1-
≥1- =
= =log2t,
=log2t,
∴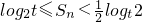 .
.
分析:(1)根据P、q是方程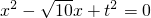 的两实根,利用韦达定理可求得p+q,pq,p,p-q,q成等比数列,根据等比中项的定义可得(p-q)2=pq,然后配凑成韦达定理的形式,即可求得正数t的值;
的两实根,利用韦达定理可求得p+q,pq,p,p-q,q成等比数列,根据等比中项的定义可得(p-q)2=pq,然后配凑成韦达定理的形式,即可求得正数t的值;
(2)根据 ,利用裂项相消法可求其前n项和Sn,再利用数列的单调性可证
,利用裂项相消法可求其前n项和Sn,再利用数列的单调性可证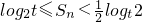 .
.
点评:此题是个中档题.考查韦达定理的应用和等比数列的性质,以及裂项相消法求数列的前n项和,体现了方程的思想.以及学生综合运用知识解决问题的能力.
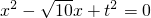 的两实根,
的两实根,∴p+q=
 ,pq=t2,
,pq=t2,∵p,p-q,q成等比数列,
∴(p-q)2=pq,即(p+q)2=5pq,
∴10=5t2,
∵t>0,∴t=
 .
.(2)∵
 =
= ,
,∴Sn=
 =1-
=1- <1=
<1=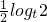 ,
,而1-
 ≥1-
≥1- =
= =log2t,
=log2t,∴
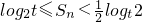 .
.分析:(1)根据P、q是方程
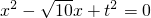 的两实根,利用韦达定理可求得p+q,pq,p,p-q,q成等比数列,根据等比中项的定义可得(p-q)2=pq,然后配凑成韦达定理的形式,即可求得正数t的值;
的两实根,利用韦达定理可求得p+q,pq,p,p-q,q成等比数列,根据等比中项的定义可得(p-q)2=pq,然后配凑成韦达定理的形式,即可求得正数t的值;(2)根据
 ,利用裂项相消法可求其前n项和Sn,再利用数列的单调性可证
,利用裂项相消法可求其前n项和Sn,再利用数列的单调性可证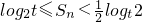 .
.点评:此题是个中档题.考查韦达定理的应用和等比数列的性质,以及裂项相消法求数列的前n项和,体现了方程的思想.以及学生综合运用知识解决问题的能力.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
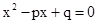 的两个实根,数列
的两个实根,数列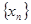 满足
满足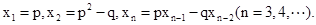

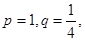 求
求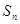 。
。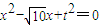 的两实根,且p,p-q,q成等比数列.
的两实根,且p,p-q,q成等比数列.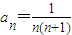 ,Sn为数列{an}的前n项和.求证:
,Sn为数列{an}的前n项和.求证: .
.