题目内容
(本小题满分12分)
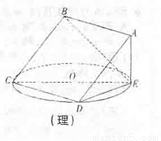
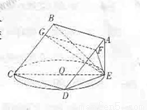
如右图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,圆O的直径为9。
(1)求证:平面ABCD 平在ADE;
平在ADE;
(2)求二面角D—BC—E的平面角的正切值;
(1)略
(2)二面角D—BC—E的平面角的正切值为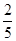
【解析】(1)证明: 垂直于圆O所在平面,CD在圆O所在平面上,
垂直于圆O所在平面,CD在圆O所在平面上,

在正方形ABCD中,CD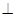 AD
AD
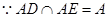
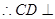 平面ADE
平面ADE
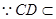 平面ABCD
平面ABCD
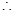 平面ABCD
平面ABCD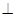 平面ADE…………4分
平面ADE…………4分
(2)解法一: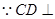 平面ADE,
平面ADE,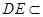 平面ADE,
平面ADE,

 CE为圆O的直径,即CE=9…………6分
CE为圆O的直径,即CE=9…………6分
设正方形ABCD的边长为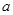
在 中,
中,
在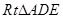 中,
中,
由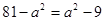 ,解得
,解得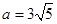
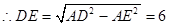 …………8分
…………8分
过点E作EF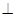 AD于点F,作FG
AD于点F,作FG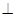 BC交BC于点G,连结GE
BC交BC于点G,连结GE
 平面ABCD
平面ABCD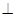 平面ADE
平面ADE
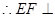 平面ABCD
平面ABCD
又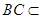 平面ABCD,
平面ABCD,
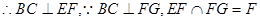
 平面EFG
平面EFG
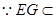 平面EFG,
平面EFG,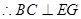
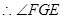 是二面角D—BC—E的平面角…………10分
是二面角D—BC—E的平面角…………10分
在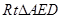 中,
中,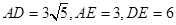
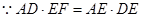

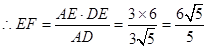
在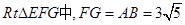
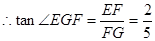
故二面角D—BC—E的平面角的正切值为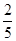 …………12分
…………12分
解法2: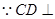 平面ADE,
平面ADE,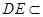 平面ADE
平面ADE

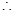 CE为圆O的直径,即CE=9…………6分
CE为圆O的直径,即CE=9…………6分
设正方形ABCD的边长为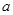
在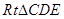 中,
中,
在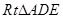 中,
中,
由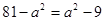 ,解得
,解得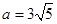
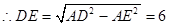 …………8分
…………8分
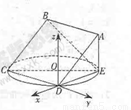 以D为坐标原点,分中辊以ED、CD所在的直线为
以D为坐标原点,分中辊以ED、CD所在的直线为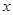 轴,
轴, 轴建立如下图所示的空间直角坐标系,则D(0,0,0),E(-6,0,0),C(0,
轴建立如下图所示的空间直角坐标系,则D(0,0,0),E(-6,0,0),C(0, ,0),A(-6,0,3),B(-6,
,0),A(-6,0,3),B(-6, ,3)
,3)
设平面ABCD的法向量为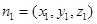
则
取 ,则
,则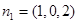 是平面ABCD的一个法向量
是平面ABCD的一个法向量
设平面BCE的法向量为
则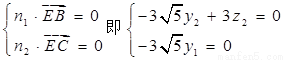
取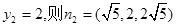 是平面ABCD的一个法向量
是平面ABCD的一个法向量
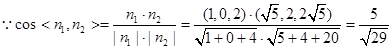
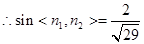
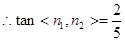 …………11分
…………11分
故二面角D—BC—E的平面角的正切值为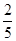 …………12分
…………12分

 中考解读考点精练系列答案
中考解读考点精练系列答案