题目内容
圆x2+y2=1上的点到直线x-y=8的距离的最小值 ．
【答案】分析：以原点为圆心1为半径的圆上的点到直线y=x-8的距离最小值，等于原点到该直线的距离减去半径1，即可得到结论．
解答：
解：圆x2+y2=1的圆心为（0，0），半径为1
由题意，以原点为圆心1为半径的圆上的点到直线y=x-8的距离最小值，等于原点到该直线的距离减去半径1
∵原点到该直线的距离为
=
∴圆x2+y2=1上的点到直线x-y=8的距离的最小值是
故答案为：
．
点评：本题考查点到直线的距离公式的运用，考查学生的计算能力，属于基础题．
解答：
解：圆x2+y2=1的圆心为（0，0），半径为1由题意，以原点为圆心1为半径的圆上的点到直线y=x-8的距离最小值，等于原点到该直线的距离减去半径1
∵原点到该直线的距离为
=∴圆x2+y2=1上的点到直线x-y=8的距离的最小值是
故答案为：
．点评：本题考查点到直线的距离公式的运用，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设P为圆x2+y2=1上的动点，过P作x轴的垂线，垂足为Q，若
=λ
，（其中λ为正常数），则点M的轨迹为（ ）
| PM |
| MQ |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
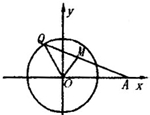如图，已知定点A（2，0），点Q是圆x2+y2=1上的动点，∠AOQ的平分线交AQ于M，当Q点在圆上移动时，求动点M的轨迹方程．