题目内容
已知函数f(x)=x2+(lga+2)x+lgb,满足f(-1)=-2,且对于任意x∈R,恒有f(x)≥2x成立。
(1)求实数a,b的值;
(2)解不等式f(x)<x+5。
(1)求实数a,b的值;
(2)解不等式f(x)<x+5。
解:(1)由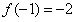 ,知
,知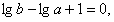
∴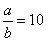 ,
,
又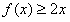 恒成立,即
恒成立,即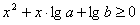 恒成立,
恒成立,
故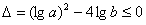 ,
,
将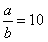 代入,得
代入,得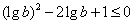 ,即
,即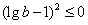 ,
,
即lgb=1,故b=10,a=100。
(2)因为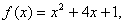
所以,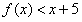 ,即
,即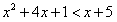 ,
,
∴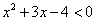 ,
,
解得:-4<x<1,
∴不等式的解集为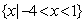 。
。
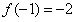 ,知
,知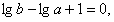
∴
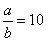 ,
,又
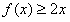 恒成立,即
恒成立,即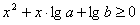 恒成立,
恒成立,故
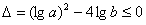 ,
,将
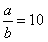 代入,得
代入,得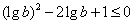 ,即
,即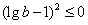 ,
,即lgb=1,故b=10,a=100。
(2)因为
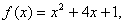
所以,
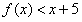 ,即
,即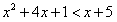 ,
,∴
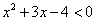 ,
,解得:-4<x<1,
∴不等式的解集为
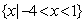 。
。
练习册系列答案
相关题目