题目内容
在△ABC中,cosA= 且cosB=
且cosB= ,则cosC等于
,则cosC等于
- A.-
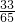
- B.
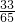
- C.-

- D.

B
分析:在△ABC中,A+B+C=π,C=π-(A+B),从而有cosC=cos[π-(A+B)]=-cos(A+B),利用两角和的余弦公式展开计算即可.
解答:∵在△ABC中,A+B+C=π,
∴C=π-(A+B),又cosA= ,cosB=
,cosB= ,
,
∴sinA= ,sinB=
,sinB= ,
,
∴cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB=(- )•
)• +
+ •
• =
=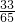 .
.
故选B.
点评:本题考查两角和与差的余弦函数,着重考查同角三角函数间的基本关系及两角和的余弦公式,属于中档题.
分析:在△ABC中,A+B+C=π,C=π-(A+B),从而有cosC=cos[π-(A+B)]=-cos(A+B),利用两角和的余弦公式展开计算即可.
解答:∵在△ABC中,A+B+C=π,
∴C=π-(A+B),又cosA=
 ,cosB=
,cosB= ,
,∴sinA=
 ,sinB=
,sinB= ,
,∴cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB=(-
 )•
)• +
+ •
• =
=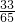 .
.故选B.
点评:本题考查两角和与差的余弦函数,着重考查同角三角函数间的基本关系及两角和的余弦公式,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
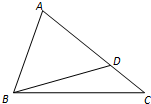 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=