题目内容
(本小题满分12分)
如图,圆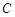 与
与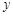 轴相切于点
轴相切于点 ,与
,与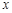 轴正半轴相交于两点
轴正半轴相交于两点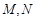 (点
(点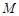 在点
在点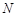 的左侧),且
的左侧),且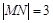 .
.
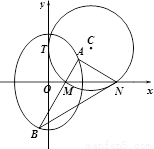
(Ⅰ)求圆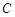 的方程;
的方程;
(Ⅱ)过点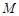 任作一条直线与椭圆
任作一条直线与椭圆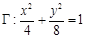 相交于
相交于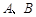 两点,连接
两点,连接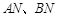 ,求证:
,求证: .
.
(Ⅰ)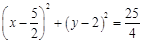 .(Ⅱ)见解析。
.(Ⅱ)见解析。
【解析】(I)由于圆 与
与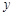 轴相切于点
轴相切于点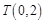 , 所以圆心坐标为
, 所以圆心坐标为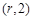 ,然后根据
,然后根据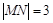
建立关于r的方程求出r值,圆的标准确定.
(2)将y=0代入圆的方程求出M,N的坐标,然后再分两种情况证明.
(i) 当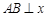 轴时,由椭圆对称性可知
轴时,由椭圆对称性可知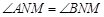 .
.
当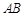 与
与 轴不垂直时,可设直线
轴不垂直时,可设直线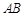 的方程为
的方程为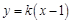 .证明
.证明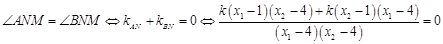 ,然后直线方程与椭圆方程联立借助韦达定理来解决即可.
,然后直线方程与椭圆方程联立借助韦达定理来解决即可.
(Ⅰ)设圆 的半径为
的半径为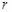 (
(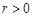 ),依题意,圆心坐标为
),依题意,圆心坐标为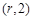 .································ 1分
.································ 1分
∵ 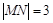
∴ 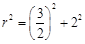 ,解得
,解得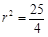 .····································································· 3分
.····································································· 3分
∴ 圆 的方程为
的方程为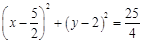 .······················································· 5分
.······················································· 5分
(Ⅱ)把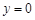 代入方程
代入方程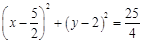 ,解得
,解得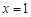 ,或
,或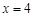 ,
,
即点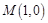 ,
,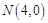 .····················································································· 6分
.····················································································· 6分
(1)当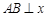 轴时,由椭圆对称性可知
轴时,由椭圆对称性可知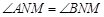 .······························· 7分
.······························· 7分
(2)当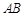 与
与 轴不垂直时,可设直线
轴不垂直时,可设直线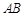 的方程为
的方程为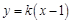 .
.
联立方程 ,消去
,消去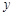 得,
得, .······················ 8分
.······················ 8分
设直线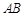 交椭圆
交椭圆 于
于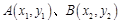 两点,则
两点,则
 ,
,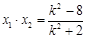 .······································································· 9分
.······································································· 9分
∵ 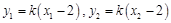 ,
,
∴ 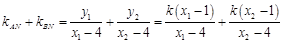
 .······························································· 10分
.······························································· 10分
∵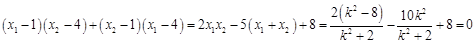 ,
,
11分
∴  ,
,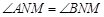 .····························································· 12分
.····························································· 12分
综上所述,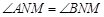 . 13分
. 13分
