题目内容
已知函数f(x)=(a+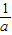 )lnx+
)lnx+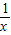 -x(a>1).
-x(a>1).(l)试讨论f(x)在区间(0,1)上的单调性;
(2)当a∈[3,+∞)时,曲线y=f(x)上总存在相异两点P(x1,f(x1)),Q(x2,f (x2 )),使得曲线y=f(x)在点P,Q处的切线互相平行,求证:x1+x2>
 .
.
【答案】分析:(1)求出f′(x),当x∈(0,1)时,解不等式f′(x)>0,f′(x)<0即可.
(2)由题意可得,当a∈[3,+∞)时,f′(x1)=f′(x2)(x1,x2>0,且x1≠x2),由此可得a+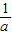 =
=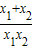 >
>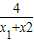 ,从而
,从而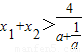 ,只要求出
,只要求出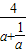 在[3,+∞)的最大值即可.
在[3,+∞)的最大值即可.
解答:解:(1)由已知,得x>0,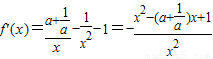 =-
=-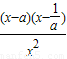 .
.
由f′(x)=0,得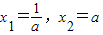 .因为a>1,所以0
.因为a>1,所以0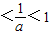 ,且a
,且a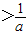 .
.
所以在区间(0,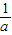 )上,f′(x)<0;在区间(
)上,f′(x)<0;在区间(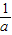 ,1)上,f′(x)>0.
,1)上,f′(x)>0.
故f(x)在(0,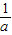 )上单调递减,在(
)上单调递减,在(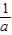 ,1)上单调递增.
,1)上单调递增.
证明:(2)由题意可得,当a∈[3,+∞)时,f′(x1)=f′(x2)(x1,x2>0,且x1≠x2).
即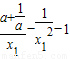 =
=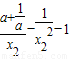 ,所以a+
,所以a+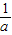 =
=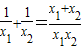 ,a∈[3,+∞).
,a∈[3,+∞).
因为x1,x2>0,且x1≠x2,所以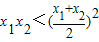 恒成立,
恒成立,
所以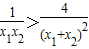 ,又x1+x2>0,所以
,又x1+x2>0,所以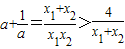 ,整理得
,整理得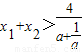 ,
,
令g(a)=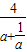 ,因为a∈[3,+∞),所以a+
,因为a∈[3,+∞),所以a+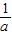 单调递增,g(a)单调递减,
单调递增,g(a)单调递减,
所以g(a)在[3,+∞)上的最大值为g(3)= ,
,
所以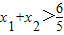 .
.
点评:本题考查了利用导数研究函数的单调性问题、求最值问题,运用所学知识解决问题的能力.
(2)由题意可得,当a∈[3,+∞)时,f′(x1)=f′(x2)(x1,x2>0,且x1≠x2),由此可得a+
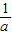 =
=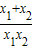 >
>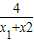 ,从而
,从而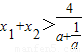 ,只要求出
,只要求出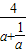 在[3,+∞)的最大值即可.
在[3,+∞)的最大值即可.解答:解:(1)由已知,得x>0,
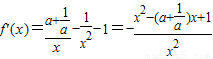 =-
=-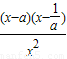 .
.由f′(x)=0,得
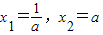 .因为a>1,所以0
.因为a>1,所以0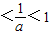 ,且a
,且a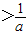 .
.所以在区间(0,
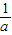 )上,f′(x)<0;在区间(
)上,f′(x)<0;在区间(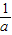 ,1)上,f′(x)>0.
,1)上,f′(x)>0.故f(x)在(0,
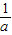 )上单调递减,在(
)上单调递减,在(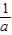 ,1)上单调递增.
,1)上单调递增.证明:(2)由题意可得,当a∈[3,+∞)时,f′(x1)=f′(x2)(x1,x2>0,且x1≠x2).
即
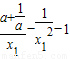 =
=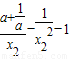 ,所以a+
,所以a+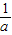 =
=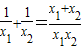 ,a∈[3,+∞).
,a∈[3,+∞).因为x1,x2>0,且x1≠x2,所以
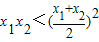 恒成立,
恒成立,所以
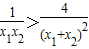 ,又x1+x2>0,所以
,又x1+x2>0,所以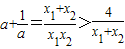 ,整理得
,整理得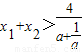 ,
,令g(a)=
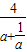 ,因为a∈[3,+∞),所以a+
,因为a∈[3,+∞),所以a+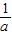 单调递增,g(a)单调递减,
单调递增,g(a)单调递减,所以g(a)在[3,+∞)上的最大值为g(3)=
 ,
,所以
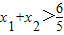 .
.点评:本题考查了利用导数研究函数的单调性问题、求最值问题,运用所学知识解决问题的能力.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|