题目内容
已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则公差为
3
解析试题分析:因为30-15=(a2-a1)+(a4-a3)+…+(a10-a9)=5d,所以d=3,故答案为:3 .
考点:等差数列的前n项和.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知等差数列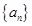 的前n项和为
的前n项和为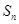 ,满足
,满足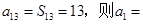 ( )
( )
A.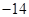 | B.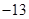 | C.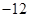 | D.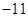 |
等差数列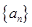 的前
的前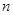 项和为
项和为 ,且
,且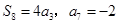 ,则
,则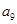 为( )
为( )
| A.-6 | B.-4 | C.-2 | D.2 |
数列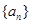 为等差数列,
为等差数列, 为等比数列,
为等比数列, ,则
,则 ( )
( )
A. | B.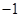 | C. | D. |
等差数列 ,
, 的前
的前 项和分别为
项和分别为 ,
, ,若
,若 ,则
,则 ( )
( )
A. | B. | C. | D. |
在等差数列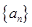 中,若
中,若 ,则
,则 ( )
( )
| A.45 | B.75 | C.180 | D.320 |
将1,2,…,9这9个数平均分成三组,则每组的三个数都可以成等差数列的概率为( )
A. | B. | C. | D. |
数列{an}的通项公式是an= ,若前n项和为10,则项数n为( )
,若前n项和为10,则项数n为( )
| A.120 |
| B.99 |
| C.110 |
| D.121 |
已知等差数列{an},且3(a3+a5)+2(a7+a10+a13)=48,则数列{an}的前13项之和为( )
| A.24 | B.39 | C.104 | D.52 |