Question

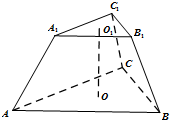正三棱台ABC-A₁B₁C₁中，O，O₁分别是上、下底面的中心．已知A1B1=O1O=

3

，AB=2

3

．
（1）求正三棱台ABC-A₁B₁C₁的体积；
（2）求正三棱台ABC-A₁B₁C₁的侧面积．

Answer 1

分析：根据三棱台的体积公式和侧面积公式分别计算体积和侧面积即可．

解答：解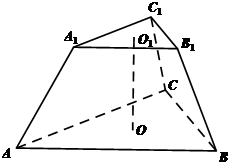：（1）正三棱台ABC-A₁B₁C₁的上底面积为
S△ABC=

3

4

×(

3

)2=

3 3

4

，
下底面积为S△A1B1C1=

3

4

×(2

3

)2=3

3

．
所以正三棱台ABC-A₁B₁C₁的体积为
VABC-A1B1C1=

1

3

（S△ABC+

S△ABC•S△A1B1C1

+S△A1B1C1）=

1

3

(

3 3

4

+

3 3

2

+3

3

)•

3

=

21

4

．
（2）设A₁B₁，AB的中点分别为M₁，M，
则正三棱台ABC-A₁B₁C₁的斜高为M1M=

( 3 )2+( 1 2 )2

=

13

2

，
故正三棱台ABC-A₁B₁C₁的侧面积为S侧=3×[

1

2

×(

3

+3

3

)×

13

2

]=3

39

．

点评：本题主要考查棱台的体积和侧面积的计算要求熟练掌握相应的体积公式和侧面积公式．考查学生的计算能力．