题目内容
已知函数
（1）试判断函数的单调性并加以证明；
（2）当f（x）＜a恒成立时，求实数a的取值范围．
【答案】分析：（1）可得函数的定义域为R，再利用单调性的定义，按照取值、作差、变形、定号下结论的步骤进行正面；
（2）将函数整理为
，从而可求出函数的值域，进而可确定实数a的取值范围．
解答：解：（1）函数
的定义域为R，
函数f（x）在R上是增函数，
设x1，x2是R内任意两个值，并且x1＜x2
则
=
=
…（5分）
∵x1＜x2∴
∴
．
即∴f（x1）＜f（x2）
∴f（x）是R上的增函数．…（7分）
（2）
∵2x＞0∴2x+1＞1
∴
，
∴
，
∴
即-1＜f（x）＜1…（10分）
当f（x）＜a恒成立时，a≥1…（12分）
点评：本题以函数为载体，考查单调性的判断与证明，考查函数的值域，考查恒成立问题，属于中档题．
（2）将函数整理为
，从而可求出函数的值域，进而可确定实数a的取值范围．解答：解：（1）函数
的定义域为R，函数f（x）在R上是增函数，
设x1，x2是R内任意两个值，并且x1＜x2
则
==…（5分）∵x1＜x2∴
∴
．即∴f（x1）＜f（x2）
∴f（x）是R上的增函数．…（7分）
（2）
∵2x＞0∴2x+1＞1
∴
，∴
，∴
即-1＜f（x）＜1…（10分）
当f（x）＜a恒成立时，a≥1…（12分）
点评：本题以函数为载体，考查单调性的判断与证明，考查函数的值域，考查恒成立问题，属于中档题．
练习册系列答案
相关题目
的奇偶性；
.
.
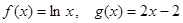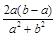（闭区间[m，n]的长度定义为n –m）．
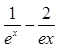是否存在实数根？说明理由。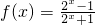
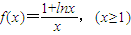
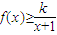恒成立，求实数k的取值范围；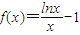
．
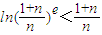