题目内容
设数列{an}满足an=2an-1+1（n≥2），且a1=1，bn=log2（an+1）
（1）证明：数列{an+1}为等比数列；
（2）求数列{
}的前n项和Sn．
（1）证明：因为an=2an-1+1（n≥2），所以an+1=2（an-1+1）（n≥2），
所以数列{an+1}是公比为2的等比数列．
（2）因为数列{an+1}是首项为a1+1=2，公比为2的等比数列，
所以an+1=2•2n-1=2n，所以bn=log2（an+1）=n．
所以=
=
（
）．
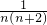所以Sn=（1-
）+（-
）+（-
）+…+（
-
）+（
-
）
=（1+--）=
．
分析：（1）根据等比数列的定义证明：由an=2an-1+1（n≥2），得an+1=2（an-1+1）（n≥2），从而得证；
（2）先求出bn=n，进而得到=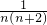，利用裂项相消法即可求出Sn．
点评：本题考查等比数列的定义、裂项相消法求数列的前n项和，考查学生分析问题解决问题的能力．
所以数列{an+1}是公比为2的等比数列．
（2）因为数列{an+1}是首项为a1+1=2，公比为2的等比数列，
所以an+1=2•2n-1=2n，所以bn=log2（an+1）=n．
所以
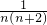==（）．所以Sn=
（1-）+（-）+（-）+…+（-）+（-）=
（1+--）=．分析：（1）根据等比数列的定义证明：由an=2an-1+1（n≥2），得an+1=2（an-1+1）（n≥2），从而得证；
（2）先求出bn=n，进而得到
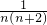=，利用裂项相消法即可求出Sn．点评：本题考查等比数列的定义、裂项相消法求数列的前n项和，考查学生分析问题解决问题的能力．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设数列{an}满足a1=1，a2+a4=6，且对任意n∈N*，函数f（x）=（an-an+1+an+2）x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
，则数列{cn}的前n项和Sn为（ ）
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|