题目内容
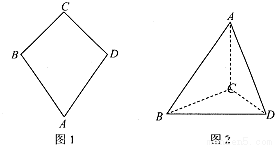
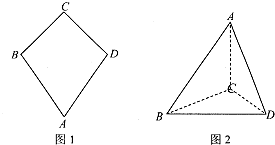 如图一,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2.把△ABD沿BD折起(如图二),使二面角A-BD-C的余弦值等于
如图一,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2.把△ABD沿BD折起(如图二),使二面角A-BD-C的余弦值等于
| ||
| 3 |
(Ⅰ)求A,C两点间的距离;
(Ⅱ)证明:AC⊥平面BCD;
(Ⅲ)求直线AC与平面ABD所成角的正弦值.
分析:(I)取BD的中点E,先证得∠AEC就是二面角A-BD-C的平面角,再在△ACE中利用余弦定理即可求得A,C两点间的距离;
(II)欲证线面垂直:AC⊥平面BCD,转化为证明线线垂直:AC⊥BC,AC⊥CD,即可;
(III)欲求直线AC与平面ABD所成角,先结合(I)中的垂直关系作出直线AC与平面ABD所成角,最后利用直角三角形中的边角关系即可求出所成角的正弦值.
(II)欲证线面垂直:AC⊥平面BCD,转化为证明线线垂直:AC⊥BC,AC⊥CD,即可;
(III)欲求直线AC与平面ABD所成角,先结合(I)中的垂直关系作出直线AC与平面ABD所成角,最后利用直角三角形中的边角关系即可求出所成角的正弦值.
解答:解:(Ⅰ)取BD的中点E,连接AE,CE,
由AB=AD,CB=CD,得:AE⊥BD,CE⊥BD
∴∠AEC就是二面角A-BD-C的平面角,
∴cos∠AEC=
(2分)
在△ACE中,AE=
, CE=
AC2=AE2+CE2-2AE•CE•cos∠AEC
=6+2-2×
×
×
=4
∴AC=2(4分)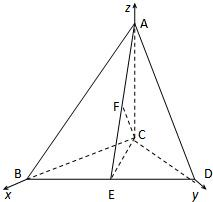
(Ⅱ)由AC=AD=BD=2
,AC=BC=CD=2
∴AC2+BC2=AB2,AC2+CD2=AD2,
∴∠ACB=∠ACD=90°(6分)
∴AC⊥BC,AC⊥CD,
又BC∩CD=C∴AC⊥平面BCD.(8分)
(Ⅲ)由(Ⅰ)知BD⊥平面ACEBD?平面ABD
∴平面ACE⊥平面ABD(10分)
平面ACE∩平面ABD=AE,
作CF⊥AE交AE于F,则CF⊥平面ABD,∠CAF就是AC与平面ABD所成的角,(12分)
∴sin∠CAF=sin∠CAE=
=
.(14分)
由AB=AD,CB=CD,得:AE⊥BD,CE⊥BD
∴∠AEC就是二面角A-BD-C的平面角,
∴cos∠AEC=
| ||
| 3 |
在△ACE中,AE=
| 6 |
| 2 |
AC2=AE2+CE2-2AE•CE•cos∠AEC
=6+2-2×
| 6 |
| 2 |
| ||
| 3 |
∴AC=2(4分)

(Ⅱ)由AC=AD=BD=2
| 2 |
∴AC2+BC2=AB2,AC2+CD2=AD2,
∴∠ACB=∠ACD=90°(6分)
∴AC⊥BC,AC⊥CD,
又BC∩CD=C∴AC⊥平面BCD.(8分)
(Ⅲ)由(Ⅰ)知BD⊥平面ACEBD?平面ABD
∴平面ACE⊥平面ABD(10分)
平面ACE∩平面ABD=AE,
作CF⊥AE交AE于F,则CF⊥平面ABD,∠CAF就是AC与平面ABD所成的角,(12分)
∴sin∠CAF=sin∠CAE=
| CE |
| AE |
| ||
| 3 |
点评:本题主要考查了点、线、面间的距离计算、直线与平面垂直的判定、直线与平面所成的角,以及空间几何体的概念、空间想象力,是中等题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,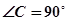 ,
,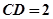 。
。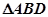 沿BD折起(如图二),使二面角A-BD-C的余弦值等于
沿BD折起(如图二),使二面角A-BD-C的余弦值等于 。对于图二,
。对于图二,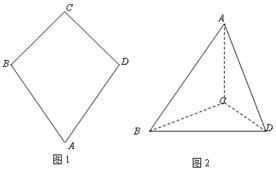
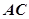 的长,并证明:
的长,并证明: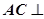 平面
平面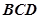 ;
;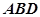 所成角的正弦值。
所成角的正弦值。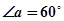 ,
,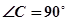 ,
,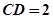 。
。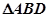 沿BD折起(如图二),使二面角A-BD-C的余弦值等于
沿BD折起(如图二),使二面角A-BD-C的余弦值等于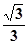 。对于图二,
。对于图二,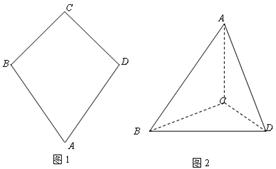
 的长,并证明:
的长,并证明: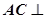 平面
平面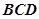 ;
;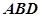 所成角的正弦值。
所成角的正弦值。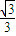 .对于图二,完成以下各小题:
.对于图二,完成以下各小题: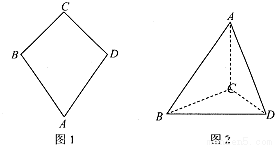
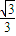 .对于图二,完成以下各小题:
.对于图二,完成以下各小题: