题目内容
如图，直角梯形ABCD中，AD⊥AB，AB∥DC，AB=4，AD=DC=2，设点N是DC边的中点，点M是梯形ABCD内或边界上的一个动点，则| AM |
| AN |
分析：以直线AB为x轴、AD为y轴，建立如图所示直角坐标系，然后求出A、B、C、D、N各点的坐标．设M（x，y），根据数量积的坐标运算公式可得
•
=x+2y，设z=x+2y对应直线l，将直线l进行平移，可得当它经过点C（2，2）时目标函数z达到最大值，由此即可得到
•
的最大值．
| AM |
| AN |
| AM |
| AN |
解答：解：以直线AB为x轴，AD为y轴建立如图所示直角坐标系，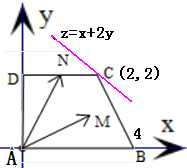
可得A（0，0），B（4，0），C（2，2），D（0，2），N（1，2）
设M（x，y），可得
=（x，y），
=（1，2），
∴
•
=x+2y，设z=x+2y对应直线l，
将直线l平移，得当它经过点C（2，2）时，目标函数z达到最大值
∴z=x+2y的最大值为2+2×2=6，即
•
的最大值是6
故答案为：6
可得A（0，0），B（4，0），C（2，2），D（0，2），N（1，2）
设M（x，y），可得
| AM |
| AN |
∴
| AM |
| AN |
将直线l平移，得当它经过点C（2，2）时，目标函数z达到最大值
∴z=x+2y的最大值为2+2×2=6，即
| AM |
| AN |
故答案为：6
点评：本题给出直角梯形中的向量，求它们数量积的最大值．着重考查了向量数量积的定义和运用直线平移法求“二元一次型”目标函数的最值等知识，同时考查了学生对向量数量积几何意义灵活应用能力，属于中档题．
练习册系列答案
相关题目
（2014•宜宾一模）如图，直角梯形ABCD中，∠ABC=∠BAD=90°，AB=BC且△ABC的面积等于△ADC面积的
（2013•惠州一模）如图，直角梯形ACDE与等腰直角△ABC所在平面互相垂直，F为BC的中点，∠BAC=∠ACD=90°，AE∥CD，DC=AC=2AE=2
．梯形ABCD所在平面外有一点P，满足PA⊥平面ABCD，PA=PB．