题目内容
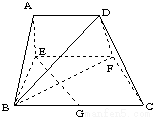
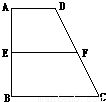
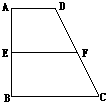
已知在直角梯形ABCD中,AD∥BC,∠ABC=| π | 2 |
(1)若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值.
(2)当f(x)取得最大值时,求BD与平面BCFE所成角的正弦值.


分析:(1)先表示出三棱锥的体积记为f(x),利用基本不等式求出f(x)的最大值.
(2)先表示出BD与平面BCFE所成角,然后解直角三角形的边长,求出BD与平面BCFE所成角的正弦值.
(2)先表示出BD与平面BCFE所成角,然后解直角三角形的边长,求出BD与平面BCFE所成角的正弦值.
解答: 解:(1)因为ABCD为直角梯形,沿EF将梯形ABCD翻折后,平面AEFD⊥平面EBCF;所以三棱锥D-BCF的高为AE所以三棱锥D-BCF的体积为:f(x)=
解:(1)因为ABCD为直角梯形,沿EF将梯形ABCD翻折后,平面AEFD⊥平面EBCF;所以三棱锥D-BCF的高为AE所以三棱锥D-BCF的体积为:f(x)=
×
×4×(4-x)×x(4分)
所以f(x)=
(4-x)x≤
(
)2=
所以当x=2时,f(x)取最大值为
(7分)
(2)作DH⊥EF于H,连接HB,
因为平面AEFD⊥平面EBCF;
所以DH⊥面BCFE,所以∠DBH就是所求的BD与平面BCFE所成角(10分)
容易计算得,DH=2,BH=
=2
,R所以BD=
=2
所以sin∠DBH=
=
(13分)
所以,BD与平面BCFE所成角的正弦值为
(14分)
 解:(1)因为ABCD为直角梯形,沿EF将梯形ABCD翻折后,平面AEFD⊥平面EBCF;所以三棱锥D-BCF的高为AE所以三棱锥D-BCF的体积为:f(x)=
解:(1)因为ABCD为直角梯形,沿EF将梯形ABCD翻折后,平面AEFD⊥平面EBCF;所以三棱锥D-BCF的高为AE所以三棱锥D-BCF的体积为:f(x)=| 1 |
| 3 |
| 1 |
| 2 |
所以f(x)=
| 2 |
| 3 |
| 2 |
| 3 |
| 4-x+x |
| 2 |
| 8 |
| 3 |
所以当x=2时,f(x)取最大值为
| 8 |
| 3 |
(2)作DH⊥EF于H,连接HB,
因为平面AEFD⊥平面EBCF;
所以DH⊥面BCFE,所以∠DBH就是所求的BD与平面BCFE所成角(10分)
容易计算得,DH=2,BH=
| BE2+EH2 |
| 2 |
| DH2+BH2 |
| 3 |
所以sin∠DBH=
| DH |
| BD |
| ||
| 3 |
所以,BD与平面BCFE所成角的正弦值为
| ||
| 3 |
点评:本题考查棱锥的体积,函数的最值,直线与平面所成的角,考查空间想象能力,是中档题.

练习册系列答案
相关题目
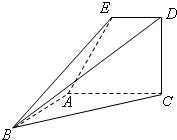 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE. 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC=
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC= ,AB=BC=2AD=4,E、F分别是两腰AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).
,AB=BC=2AD=4,E、F分别是两腰AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).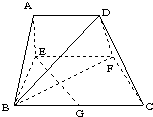
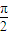 ,AB=BC=2AD=4,E、F分别是两腰AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).
,AB=BC=2AD=4,E、F分别是两腰AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).