题目内容
设 ,
,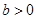 ,则当
,则当 ______时,
______时, 取得最小值.
取得最小值.
 .
.
解析试题分析: 且
且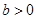 ,
, ,当
,当 时,则有
时,则有 ,
,
 ,另一方面
,另一方面
 ,
, ,
, ,当且仅当
,当且仅当 ,即
,即 且
且 时,即当
时,即当 时,
时, 取得最小值
取得最小值 ,此时
,此时 ;当
;当 ,则有
,则有 ,
, ,另一方面
,另一方面
 ,当且仅当
,当且仅当 时,由于
时,由于 ,
,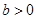 ,即当
,即当 时,由于
时,由于 ,解得
,解得 ,
, ,上式取等号,所以
,上式取等号,所以 ,即
,即 取得最小值
取得最小值 ,由于
,由于 ,故当
,故当 时,
时,
取得最小值.
考点:基本不等式

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
设 ,
,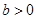 ,则当
,则当 ______时,
______时, 取得最小值.
取得最小值.
 .
.
解析试题分析: 且
且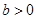 ,
, ,当
,当 时,则有
时,则有 ,
,
 ,另一方面
,另一方面
 ,
, ,
, ,当且仅当
,当且仅当 ,即
,即 且
且 时,即当
时,即当 时,
时, 取得最小值
取得最小值 ,此时
,此时 ;当
;当 ,则有
,则有 ,
, ,另一方面
,另一方面
 ,当且仅当
,当且仅当 时,由于
时,由于 ,
,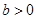 ,即当
,即当 时,由于
时,由于 ,解得
,解得 ,
, ,上式取等号,所以
,上式取等号,所以 ,即
,即 取得最小值
取得最小值 ,由于
,由于 ,故当
,故当 时,
时,
取得最小值.
考点:基本不等式

 名校课堂系列答案
名校课堂系列答案