题目内容
设点P是曲线y=x2上的一个动点,曲线y=x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=x2的另一交点为Q,则PQ的最小值为________.

设P(x0,x02),又y′=2x,则直线PQ的方程为y=-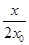 +
+ +x02.代入y=x2得x2+
+x02.代入y=x2得x2+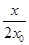 -
- -x02=0,
-x02=0,
即(x-x0) =0,所以点Q的坐标为
=0,所以点Q的坐标为 .从而PQ2=
.从而PQ2=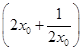 2+
2+ 2,令t=4x02,则PQ2=f(t)=t+
2,令t=4x02,则PQ2=f(t)=t+ +
+ +3(t>0),则f′(t)=
+3(t>0),则f′(t)=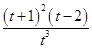 ,即f(t)在(0,2)上是减函数,在(2,+∞)上是增函数,故当t=2时,PQ有最小值
,即f(t)在(0,2)上是减函数,在(2,+∞)上是增函数,故当t=2时,PQ有最小值 .
.
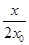 +
+ +x02.代入y=x2得x2+
+x02.代入y=x2得x2+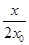 -
- -x02=0,
-x02=0,即(x-x0)
 =0,所以点Q的坐标为
=0,所以点Q的坐标为 .从而PQ2=
.从而PQ2=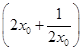 2+
2+ 2,令t=4x02,则PQ2=f(t)=t+
2,令t=4x02,则PQ2=f(t)=t+ +
+ +3(t>0),则f′(t)=
+3(t>0),则f′(t)=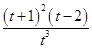 ,即f(t)在(0,2)上是减函数,在(2,+∞)上是增函数,故当t=2时,PQ有最小值
,即f(t)在(0,2)上是减函数,在(2,+∞)上是增函数,故当t=2时,PQ有最小值 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
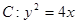 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.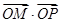 为定值;
为定值;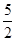 ,求向量
,求向量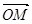 与
与 的夹角;
的夹角;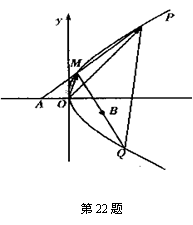
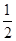 =0的距离等于( )
=0的距离等于( )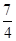 B.2 C.
B.2 C.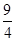 D.4
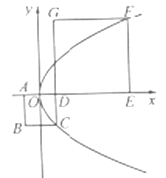
D.4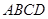 和正方形
和正方形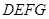 的边长分别为
的边长分别为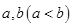 ,原点
,原点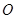 为
为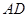 的中点,抛物线
的中点,抛物线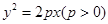 经过
经过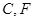 两点,则
两点,则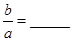 .
.
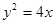 ,直线
,直线 的方程为
的方程为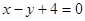 ,在抛物线上有一动点P到y轴的距离为
,在抛物线上有一动点P到y轴的距离为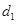 ,P到直线
,P到直线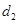 ,则
,则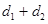 的最小值为( )
的最小值为( ) 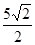


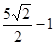
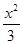 -
-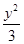 =1相交于A,B两点,若△ABF为等边三角形,则p=________.
=1相交于A,B两点,若△ABF为等边三角形,则p=________.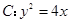 的焦点为
的焦点为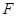 ,
,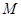 为抛物线
为抛物线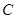 上一点,
上一点,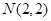 ,则
,则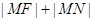 的取值范围是 .
的取值范围是 .