题目内容

20．设曲线y=eax-e-ax-4在点（0，b）处的切线与直线x+4y+1=0垂直，则2a+b=（　　）
A．-4B．-2C．0D．2

分析 求出函数的导数，求得切线的斜率，由两直线垂直的条件：斜率之积为-1，可得2a=4，再由切点在曲线上可得b=-4，即可得到所求值．

解答 解：y=eax-e-ax-4的导数为y′=aeax+ae-ax，
即有在点（0，b）处的切线斜率为k=2a，
由切线与直线x+4y+1=0垂直，
则k=2a=4，
又切点为（0，b），则b=1-1-4=-4，
即有2a+b=0，
故选：C．

点评 本题考查导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，同时考查两直线垂直的条件：斜率之积为-1，正确求导是解题的关键．

练习册系列答案
相关题目
10．已知x、y∈R+，且x+y=4，求$\frac{1}{x}$+$\frac{3}{y}$的最小值．
11．在△ABC中，已知a=$\sqrt{3}$，b=2$\sqrt{3}$，c=3，则∠A=$\frac{π}{6}$．
8．已知函数f（x）是定义在（0，+∞）上的减函数且f（m）＜f（2m-1），则m的取值范围是（$\frac{1}{2}$，1）（用区间表示）
15．已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数），曲线C2的极坐标方程为ρ=2cos（θ+$\frac{π}{3}$），曲线C3的极坐标方程为ρcos（θ-$\frac{π}{3}$）=2．
（1）若C1，C2相交于A、B两点，求出线段AB的长；
（2）求线AB的垂直平分线的极坐标方程；
（3）求曲线C2上的点到C3的最远距离．
5．已知椭圆E的长轴的一个端点是抛物线y2=4$\sqrt{5}$x的焦点，离心率是$\frac{{\sqrt{6}}}{3}$．
（1）求椭圆E的标准方程；
（2）已知动直线y=k（x+1）与椭圆E相交于A、B两点，且在x轴上存在点M，使得$\overrightarrow{MA}•\overrightarrow{MB}$与k的取值无关，试求点M的坐标．
12．已知：f（x）=x${\;}^{\frac{1}{2}}$-x${\;}^{-\frac{1}{2}}$．
（1）证明：函数f（x）有反函数，并求出反函数；
（2）反函数的图象是否经过点（0，1）？反函数的图象与y=x有无交点？
（3）设反函数为y=f-1（x），求不等式f-1（x）≤0的解集．
9．下列抽样问题中最适合用分层抽样法进行抽样的是（　　）
A．从12名学生中随机抽泣8人参加活动
B．某单位有210名员工，其中老年员工20人，中年员工40人，青年员工150人，为了解情况，要从中抽取一个容量为21的样本
C．从参加期中考试的1200名高中生随机抽取100人分析作答情况
D．从1200名观众中随机抽取3名幸运观众
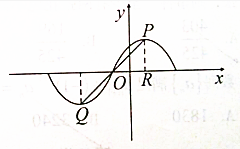10．已知函数f（x）=Acos（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$），部分图象如图所示，PQ分别为图象的最高点和最低点，PR⊥x轴于R（$\frac{1}{2}$，0）点，∠RPQ=45°，|PQ|=2$\sqrt{2}$．
（1）求f（x）的解析式；
（2）若f（m）=$\frac{3}{5}$，求sinmπ

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网