题目内容
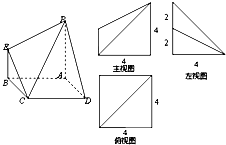 如图多面体PE-ABCD是由正方体所截得,它的三视图如图所示,则多面体的体积是VPE-ABCD=
如图多面体PE-ABCD是由正方体所截得,它的三视图如图所示,则多面体的体积是VPE-ABCD=分析:补全几何体,利用三视图的数据计算直三棱柱DPG-MCN与三棱锥P-CME的体积的体积,用正方体的体积减去棱柱,棱锥的体积,可求的要求多面体的体积.
解答:解:补全几何体是正方体如图:

连接MC,PC,则多面体DPG-MCN为直三棱柱,其体积为
×4×4×4=32;
三棱锥P-CME的体积为
×
×2×4×4=
;
正方体的体积为4×4×4=64,
∴多面体PE-ABCD的体积为64-32-
=
.
故答案是:
.

连接MC,PC,则多面体DPG-MCN为直三棱柱,其体积为
| 1 |
| 2 |
三棱锥P-CME的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
正方体的体积为4×4×4=64,
∴多面体PE-ABCD的体积为64-32-
| 16 |
| 3 |
| 80 |
| 3 |
故答案是:
| 80 |
| 3 |
点评:本题考查了用割补法求多面体的体积.考查了棱柱与棱锥的体积公式,计算要细心,属于基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
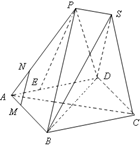 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、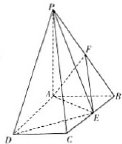 如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.