题目内容
已知函数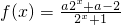 是定义在R上的奇函数.
是定义在R上的奇函数.
(1)求a的值;
(2)判断f(x)在R上的单调性并用定义证明;
(3)若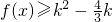 对x∈[-1,2]恒成立,求实数k的取值范围.
对x∈[-1,2]恒成立,求实数k的取值范围.
解:(1)根据题意,函数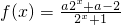 是定义在R上的奇函数,
是定义在R上的奇函数,
则有f(0)=0,即 =0,解可得a=1,
=0,解可得a=1,
即a=1;
(2)由(1)得a=1,则f(x)= =1-
=1- ,
,
设x1<x2,则f(x1)-f(x2)=(1- )-(1-
)-(1-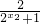 )=
)=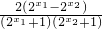 <0,
<0,
即f(x1)-f(x2)<0,
则f(x)在R上为增函数.
(3)由(2)可得,f(x)在[-1,2]上为增函数,
则f(x)在[-1,2]上的最小值为f(-1)=- ,
,
又由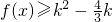 对x∈[-1,2]恒成立,
对x∈[-1,2]恒成立,
则- ≥k2-
≥k2- k,
k,
即3k2-4k+1≤0,解可得 ≤k≤1,
≤k≤1,
故实数k的取值范围是[ ,1].
,1].
分析:(1)根据题意,结合奇函数的性质,可得f(0)=0,即可得 =0,解可得a的值;
=0,解可得a的值;
(2)将a=1代入f(x)可得f(x)的解析式,设设x1<x2,再做差变形可得f(x1)-f(x2)=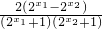 ,由指数函数的性质,判断可得f(x1)-f(x2)<0,即可得证明;
,由指数函数的性质,判断可得f(x1)-f(x2)<0,即可得证明;
(3)由(2)的结论可得,f(x)在[-1,2]上为增函数,分析可得,f(x)在[-1,2]上的最小值,结合题意可得- ≥k2-
≥k2- k,解可得答案.
k,解可得答案.
点评:本题考查函数的奇偶性与单调性的应用,涉及函数的恒成立问题,关键是理解运用单调性、奇偶性以及函数的最值之间的关系.
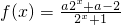 是定义在R上的奇函数,
是定义在R上的奇函数,则有f(0)=0,即
 =0,解可得a=1,
=0,解可得a=1,即a=1;
(2)由(1)得a=1,则f(x)=
 =1-
=1- ,
,设x1<x2,则f(x1)-f(x2)=(1-
 )-(1-
)-(1-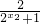 )=
)=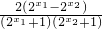 <0,
<0,即f(x1)-f(x2)<0,
则f(x)在R上为增函数.
(3)由(2)可得,f(x)在[-1,2]上为增函数,
则f(x)在[-1,2]上的最小值为f(-1)=-
 ,
,又由
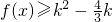 对x∈[-1,2]恒成立,
对x∈[-1,2]恒成立,则-
 ≥k2-
≥k2- k,
k,即3k2-4k+1≤0,解可得
 ≤k≤1,
≤k≤1,故实数k的取值范围是[
 ,1].
,1].分析:(1)根据题意,结合奇函数的性质,可得f(0)=0,即可得
 =0,解可得a的值;
=0,解可得a的值;(2)将a=1代入f(x)可得f(x)的解析式,设设x1<x2,再做差变形可得f(x1)-f(x2)=
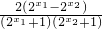 ,由指数函数的性质,判断可得f(x1)-f(x2)<0,即可得证明;
,由指数函数的性质,判断可得f(x1)-f(x2)<0,即可得证明;(3)由(2)的结论可得,f(x)在[-1,2]上为增函数,分析可得,f(x)在[-1,2]上的最小值,结合题意可得-
 ≥k2-
≥k2- k,解可得答案.
k,解可得答案.点评:本题考查函数的奇偶性与单调性的应用,涉及函数的恒成立问题,关键是理解运用单调性、奇偶性以及函数的最值之间的关系.

练习册系列答案
相关题目

 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是 .
的大小关系是 . 是定义在R上的增函数,且
是定义在R上的增函数,且 ,则m的取值范围是
.
,则m的取值范围是
. 是定义在R上的奇函数,
是定义在R上的奇函数, ,
,
 ,
,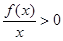 的解集是
.
的解集是
.