题目内容
函数f（x）=x3+ax2+bx+a2在x=1处有极值10，求a、b的值．
解：∵f（x）=x3+ax2+bx+a2，∴f′（x）=3x2+2ax+b，
∵函数f（x）=x3+ax2+bx+a2在x=1处有极值10，
∴
，解得
，或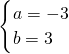
，
当时，f′（x）=3x2+8x-11=（3x+11）（x-1），
当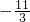
＜x＜1时，f′（x）＜0，当x＞1时，f′（x）＞0，满足x=1处为极值点；
当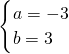时，f′（x）=3x2-6x+3=3（x-1）2，易知在x=1的两侧f′（x）＞0，
故x=1不是极值点，应舍去．
故只有满足题意．
分析：由题意可得，解之可得a，b的值，验证需满足在x=1的两侧单调性相反，即导数异号才为极值点．
点评：本题考查函数在某点取得极值的条件，注意验证是解决问题的关键，属中档题．
∵函数f（x）=x3+ax2+bx+a2在x=1处有极值10，
∴
，解得，或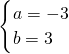，当
时，f′（x）=3x2+8x-11=（3x+11）（x-1），当
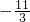＜x＜1时，f′（x）＜0，当x＞1时，f′（x）＞0，满足x=1处为极值点；当
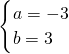时，f′（x）=3x2-6x+3=3（x-1）2，易知在x=1的两侧f′（x）＞0，故x=1不是极值点，应舍去．
故只有
满足题意．分析：由题意可得
，解之可得a，b的值，验证需满足在x=1的两侧单调性相反，即导数异号才为极值点．点评：本题考查函数在某点取得极值的条件，注意验证是解决问题的关键，属中档题．
练习册系列答案
相关题目