Question

已知直线y=k（x+1）（k＞0）与函数y=|sinx|的图象恰有四个公共点A（x₁，y₁），B（x₂，y₂），
C（x₃，y₃），D（x₄，y₄）其中x₁＜x₂＜x₃＜x₄，则有（　　）

• A、sinx₄=1
• B、sinx₄=（x₄+1）cosx₄
• C、sinx₄=kcosx₄
• D、sinx₄=（x₄+1）tanx₄

Answer 1

分析：依题意，在同一坐标系中作出直线y=k（x+1）（k＞0）与函数y=|sinx|的图象，利用导数的几何意义可求得切线的斜率，从而将切点坐标代入直线方程（即切线方程）即可求得答案．

解答：解：∵直线y=k（x+1）（k＞0）与函数y=|sinx|的图象恰有四个公共点，如图：

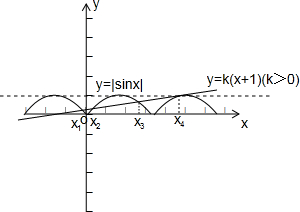
当x∈（π，2π）时，函数y=|sinx|=-sinx，y′=-cosx，
依题意，切点坐标为（x₄，y₄），
又切点处的导数值就是直线y=k（x+1）（k＞0）的斜率k，即k=-cosx₄，
又x∈（π，2π）时，|sinx₄|=-sinx₄，
∴y₄=k（x₄+1）=-cosx₄（x₄+1）=-sinx₄，
∴sinx₄=（x₄+1）cosx₄，
故选：B．

点评：本题考查正弦函数的图象，着重考查导数的几何意义的应用，考查等价转化思想与数形结合思想的综合应用，考查作图能力与分析、运算能力，属于难题．