题目内容
已知数列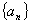 满足
满足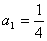 ,
,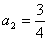 ,
,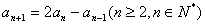 ,数列
,数列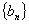 满足
满足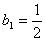 ,
, 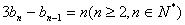
(1)求数列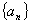 的通项公式;
的通项公式;
(2)证明:数列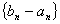 为等比数列,并求出数列
为等比数列,并求出数列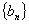 的通项公式.
的通项公式.
(1)由an+1=2an-an-1(n≥2,n∈N*),
可得an+1-an=an-an-1(n≥2,n∈N*).
∴数列{an}是首项为a1=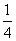 ,公差为d=a2-a1=
,公差为d=a2-a1=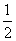 的等差数列.
的等差数列.
∴an=a1+(n-1)d=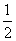 n-
n-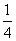 (n∈N*),
(n∈N*),
即an=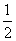 n-
n-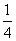 (n∈N*). (2)由3bn-bn-1=n,得bn=
(n∈N*). (2)由3bn-bn-1=n,得bn= bn-1+
bn-1+ n(n≥2,n∈N*),
n(n≥2,n∈N*),
∴bn-an= bn-1+
bn-1+ n-
n-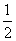 n+
n+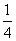 =
= bn-1-
bn-1-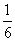 n+
n+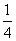 =
= (bn-1-
(bn-1-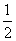 n+
n+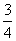 )
)
= [bn-1-
[bn-1-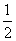 (n-1)+
(n-1)+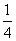 ]=
]= (bn-1-an-1).
(bn-1-an-1).
又b1-a1=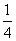 ≠0,∴bn-an≠0(n∈N*),得
≠0,∴bn-an≠0(n∈N*),得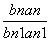 =
= (n≥2,n∈N*),
(n≥2,n∈N*),
即数列{bn-an}是首项为b1-a1=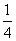 ,公比为
,公比为 的等比数列.
的等比数列.
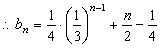

练习册系列答案
相关题目
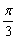 ), (x∈R)有下列命题:
), (x∈R)有下列命题: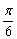 );
); <
< 的概率为
的概率为  与
与 的夹角为
的夹角为 ,
, ,
, ,若
,若 ,
, ,则实数
,则实数 的值为( )
的值为( ) B.
B. C.
C. D.
D. 
 的夹角是
的夹角是 ,
, ,
, 与
与 共线,则
共线,则 的最小值为________
的最小值为________ R,
R,
 0”的否定是
0”的否定是  0
0  R,
R, 
 上的函数
上的函数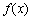 ,
, 是它的导函数,且恒有
是它的导函数,且恒有 成立,则
成立,则 B.
B.
 D.
D.
 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则 ( ).
( ). B.
B.  C.
C.  D.
D.
 ,且命题
,且命题 ,命题
,命题 ,则
,则 是
是 的
的