题目内容
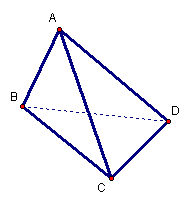
在三棱锥A－BCD中，AB，BC，CD两两互相垂直，若∠ADB＝α，∠DAC＝β，AD＝6，则当α＝30°，cos2β为何值时，三棱锥A－BCD的体积最大，最大值是多少？
答案：
解析：
解析：
|
因为AB 同理 因为AD＝6， 所以BC＝ 于是 当且仅当4 |
BC，AB
CD，BC
CD＝C，所以AB
平面ABC，所以
． (2分)
＝
，所以AB＝3，CD＝ADsin
＝6sin
， (4分)
＝
＝
＝9sin
＝
＝
，(4分)
，即
时，三棱锥A－BCD的体积取得最大值
．(2分)
练习册系列答案
相关题目
，BD＝CD＝1，另一个侧面是正三角形
,
,
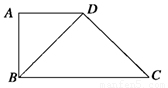
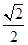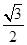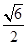则三棱锥A－BCD的外接球的体积为______________．