题目内容
已知等差数列{an}中,S3=21,S6=24,求数列{|an|}的前n项和Tn.
①当1≤n≤5时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=-n2+10n,
②当n≥6时,Tn=|a1|+…+|a5|+|a6|+…+|an|=(a1+a2+…+a5)-(a6+a7+…+an)=S5-(Sn-S5)=2S5-Sn
=n2-10n+50,
∴Tn=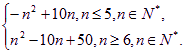
解析:
将新数列{|an|}向原有等差数列{an}靠拢转化,从而利用等差数列的性质、公式.设公差为d,则有
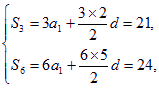 解得
解得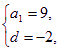
∴an=9+(n-1)×(-2)=-2n+11.
由an=-2n+11>0得n<5![]() ,
,
故{an}的前5项为正,其余各项为负.
①当1≤n≤5时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=-n2+10n,
②当n≥6时,Tn=|a1|+…+|a5|+|a6|+…+|an|=(a1+a2+…+a5)-(a6+a7+…+an)=S5-(Sn-S5)=2S5-Sn
=n2-10n+50,
∴Tn=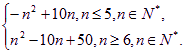

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.