题目内容
（本小题满分14分）定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时, f(x)=
.
(Ⅰ)求f(x)在[-1, 1]上的解析式;
(Ⅱ)证明f(x)在(—1, 0)上时为减函数;
(Ⅲ)当λ取何值时, 不等式f(x)＞λ在R上有解?
答案
f(x)=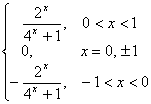
. ………………………4分
(Ⅱ) 证明略; ………………………4分
(Ⅲ) 不等式f(x)＞λ在R上有解的λ的取值范围就是λ小于f(x)在R上的最大值. 当x∈(-1, 0)时，有-
< f(x)= -
< -
；又f(x)是奇函数,当x∈(0, 1)时，f(x)在(0, 1)上也是减函数, ∴< f (x)= <.. ∴f(x)在[-1, 1]上的值域是(-, -)∪｛0｝∪(, ). 由f(x)的周期是2；故f(x)在R上的值域是(-, -)∪｛0｝∪(, )
λ＜
时，不等式f(x)＞λ在R上有解. ………………………6分
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=2，点（
）在函数
的图像上，其中
=
.
}是等比数列；
，求
及数列{
}的通项公式；
，求数列{
}的前n项和
，并证明
.
天(
)的销售价格(单位：元)为
，第
，已知该商品成本为每件25元.
关于第
的图像在点
处的切线与直线
平行.
，
满足的关系式；
上恒成立，求
（
）