题目内容
已知椭圆C1：
的一条准线方程是
，其左、右顶点分别是A、B；双曲线C2：
的一条渐近线方程为3x-5y=0。
（1）求椭圆C1的方程及双曲线C2的离心率；
（2）在第一象限内取双曲线C2上一点P，连结AP 交椭圆C1于点M，连结PB并延长交椭圆C1于点N， 若
，求
的值。
的一条准线方程是，其左、右顶点分别是A、B；双曲线C2：的一条渐近线方程为3x-5y=0。（1）求椭圆C1的方程及双曲线C2的离心率；
（2）在第一象限内取双曲线C2上一点P，连结AP 交椭圆C1于点M，连结PB并延长交椭圆C1于点N， 若
，求的值。 
解：（1）由已知
，解得：
，
∴椭圆的方程为
，双曲线的方程为
，
又
，
∴双曲线的离心率
。
（2）由（Ⅰ）A（-5，0），B（5，0），
设M
，则由
，
得M为AP的中点，∴P点坐标为
，
将M、P坐标代入C1、C2方程，得
，
消去y0，得
，解之得
或
（舍），
由此可得P（10，
），
直线PB：
，即
，
代入
得
，
∴x=
或5（舍）， ∴
，
故MN⊥x轴， 所以
。
，解得：，∴椭圆的方程为
，双曲线的方程为，又
，∴双曲线的离心率
。（2）由（Ⅰ）A（-5，0），B（5，0），
设M
，则由，得M为AP的中点，∴P点坐标为
，将M、P坐标代入C1、C2方程，得
，消去y0，得
，解之得或（舍），由此可得P（10，
），直线PB：
，即，代入
得，∴x=
或5（舍）， ∴， 故MN⊥x轴， 所以
。
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
已知椭圆C1：
+
=1（a＞b＞0）与双曲线C2：x2-
=1有公共的焦点，C2的一条渐近线与以C1的长轴为直径的圆相交于A，B两点．若C1恰好将线段AB三等分，则（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| 4 |
A、a2=
| ||
| B、a2=3 | ||
C、b2=
| ||
| D、b2=2 |
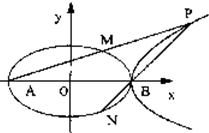如图，已知椭圆