题目内容
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
|
年份(x) |
1 |
2 |
3 |
4 |
5 |
|
人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有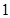 年多于10人的概率.
年多于10人的概率.
(2)根据这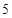 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出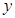 关于
关于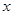 的回归方程
的回归方程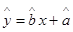 ,并计算第
,并计算第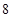 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式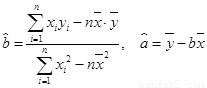
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:.(1)从这5年中任意抽取两年,共有10种抽取方法,至少有一年多于10人的事件有7种,利用古典概型的概率计算公式直接求出其概率;(2)由给出的数据,利用最小二乘法求线性回归方程系数公式求出系数,从而得到线性回归方程,再利用回归方程估计第8年的估计值.
试题解析:(1)从这5年中任意抽取两年,所有的事件有:12,13,14,15,23,24,25,34,35,45共10种,至少有1年多于10人的事件有:14,
15,24,25,34,45,45共7种,则至少有1年多于10人的概率为 .
.
(2)由已知数据得
 ,
, ,
,
则
 ,则回归直线的方程为:
,则回归直线的方程为:
则第 年的估计值为
年的估计值为 .
.
考点:本题考查了古典概型的概率公式,线性回归方程的求解和线性回归分析.

练习册系列答案
相关题目


 到
到 年十年间每年考入大学的人数.
年十年间每年考入大学的人数. 为方便计算,
为方便计算,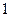 ,
,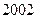 年编号为
年编号为 ,…,
,…,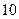 .数据如下:
.数据如下: 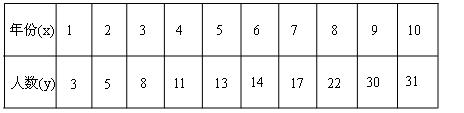
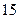 人的概率;
人的概率;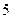 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出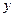 关于
关于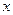 的回归方程
的回归方程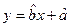 ,并计算第
,并计算第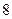 年的估计值和实际值之间的差的绝对值.
年的估计值和实际值之间的差的绝对值.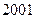 到
到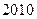 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, ,
,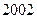 年编号为
年编号为 ,…,
,…,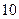 .数据如下:
.数据如下: 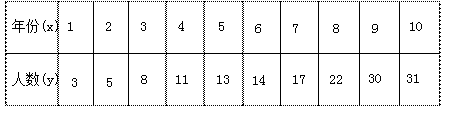
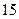 人的概率;
人的概率;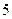 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出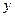 关于
关于 的回归方程
的回归方程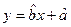 ,并计算第
,并计算第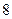 年的估计值和实际值之间的差的绝对值.
年的估计值和实际值之间的差的绝对值.