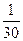题目内容
设数列{an}的首项a1=a≠ ,且
,且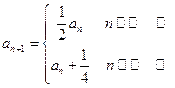 ,
,
记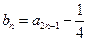 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求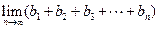
 ,且
,且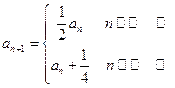 ,
,记
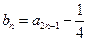 ,n==l,2,3,…·.
,n==l,2,3,…·.(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求
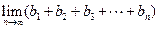
(I)a+ ,
, a+
a+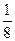
(II)见解析
(III)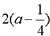
 ,
, a+
a+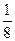
(II)见解析
(III)
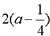
(I)a2=a1+ =a+
=a+ ,a3=
,a3= a2=
a2= a+
a+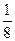 ;
;
(II)∵a4=a3+ =
= a+
a+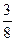 , 所以a5=
, 所以a5= a4=
a4= a+
a+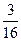 ,
,
所以b1=a1- =a-
=a- , b2=a3-
, b2=a3- =
= (a-
(a- ), b3=a5-
), b3=a5- =
= (a-
(a- ),
),
猜想:{bn}是公比为 的等比数列·
的等比数列·
证明如下:
因为bn+1=a2n+1- =
= a2n-
a2n- =
= (a2n-1-
(a2n-1- )=
)= bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为a- , 公比为
, 公比为 的等比数列·
的等比数列·
(III)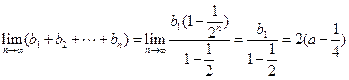
 =a+
=a+ ,a3=
,a3= a2=
a2= a+
a+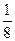 ;
;(II)∵a4=a3+
 =
= a+
a+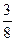 , 所以a5=
, 所以a5= a4=
a4= a+
a+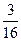 ,
,所以b1=a1-
 =a-
=a- , b2=a3-
, b2=a3- =
= (a-
(a- ), b3=a5-
), b3=a5- =
= (a-
(a- ),
),猜想:{bn}是公比为
 的等比数列·
的等比数列·证明如下:
因为bn+1=a2n+1-
 =
= a2n-
a2n- =
= (a2n-1-
(a2n-1- )=
)= bn, (n∈N*)
bn, (n∈N*)所以{bn}是首项为a-
 , 公比为
, 公比为 的等比数列·
的等比数列·(III)
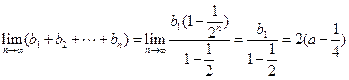

练习册系列答案
相关题目
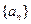 的通项公式为
的通项公式为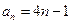 ,令
,令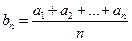 ,则数列
,则数列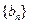 的前
的前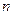 项和为
项和为



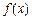 定义如下表,数列
定义如下表,数列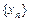 满足
满足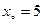 且
且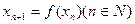 ,则
,则 .
.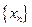 满足
满足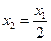 ,
,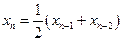 ,
,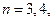 ….若
….若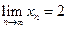 ,则( )
,则( )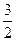 B3 C4 D5
B3 C4 D5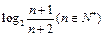 ,前n项和为Sn,则使Sn<-5成立的自然数n有
,前n项和为Sn,则使Sn<-5成立的自然数n有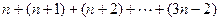 = 。
= 。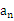 }的前n项和为
}的前n项和为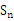 ,若
,若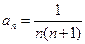 ,则
,则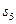 等于
等于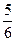 C
C 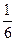 D
D