题目内容

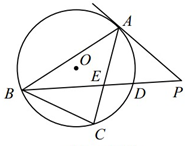（2013•深圳一模）如图，PA是⊙O的切线，A 为切点，直线 PB交⊙O于D、B两点，交弦AC 于E 点，且AE=4，EC=3，BE=6，PE=6，则 AP=
4
3
4
3
．
分析：由相交弦定理可得AE•EC=BE•ED，及AE=4，EC=3，BE=6，解得ED，即可得到PD．由PA是⊙O的切线，再由切割线定理可得PA2=PD•PB，即可解出PA．
解答：解：由相交弦定理可得：AE•EC=BE•ED，∵AE=4，EC=3，BE=6，∴4×3=6ED，解得ED=2．
∵PE=ED+PD=6，∴PD=4．
∵PA是⊙O的切线，∴PA2=PD•PB=4×（6+6）=48，∴PA=4
3
．
故答案为4
3
．
点评：熟练掌握相交弦定理和切割线定理是解题的关键．
练习册系列答案
相关题目
（2013•深圳一模）已知函数f（x）=ax+x2-xlna-b（a，b∈R，a＞1），e是自然对数的底数．
（1）试判断函数f（x）在区间（0，+∞）上的单调性；
（2）当a=e，b=4时，求整数k的值，使得函数f（x）在区间（k，k+1）上存在零点；
（3）若存在x1，x2∈[-1，1]，使得|f（x1）-f（x2）|≥e-1，试求a的取值范围．
（2013•深圳一模）（坐标系与参数方程选做题）在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．曲线C1的参数方程为
x=
t
y=t+1.
（t为参数），曲线C2的极坐标方程为ρsinθ-ρcosθ=3，则C1与C2交点在直角坐标系中的坐标为
（2，5）
（2，5）
．
（2013•深圳一模）设f（x）为定义在R上的奇函数，当x＞0时，f（x）=log3（1+x），则f（-2）=（　　）
（2013•深圳一模）已知函数f(x)=2sin(
πx
6
+
π
3
)(0≤x≤5)，点A、B分别是函数y=f（x）图象上的最高点和最低点．
（1）求点A、B的坐标以及
OA
•
OB
的值；
（2）设点A、B分别在角α、β的终边上，求tan（α-2β）的值．
（2013•深圳一模）已知数列{an}满足：a1=1，a2=a（a≠0），an+2=p•
an+12
an
（其中p为非零常数，n∈N*）．
（1）判断数列{
an+1
an
}是不是等比数列？
（2）求an；
（3）当a=1时，令bn=
nan+2
an
，Sn为数列{bn}的前n项和，求Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网