Question

已知p：方程x³+mx+4=0有两个不等的负根；q：方程4x²+4(m-2)x+1=0无实根，若p或q为真，p且q为假，求m的取值范围.

Answer 1

解：若方程x²+mx+1=0有两个不等的负根，则

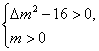解得m＞4，即p：m＞4

若方程4x²+4(m-2)x+1=0无实根，则Δ=16(m-2)²-16=16(m²-4m+3)＜0，解得1＜m＜3，即q：1＜m＜3.因p或q为真，所以p、q至少有一个为真.又p且q为假，所以p、q至少有一个为假.因此，p、q两命题应一真一假，即p为真，q为假，或p为假，q为真.

所以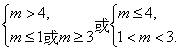解得m＞4或1＜m＜3.

温馨提示

由p、q的真假可以判断p∨q、p∧q，p的真假.反过来，由p∨q、p∧q，
p的真假也应能准确断定p、q的真假情况.如“p∧q”为假，应包括“p真q假”“p假q真”“p假q假”这三种情况.