题目内容
已知六个点A1(x1,1),B1(x2,-1),A2(x3,1),B2(x4,-1),A3(x5,1),B3(x6,-1)(x1<x2<x3<x4<x5<x6,x6-x1=5π)都在函数f(x)=sin(x+ )的图象C上.如果这六点中不同的两点的连线的中点仍在曲线C上,则称此两点为“好点组”,则上述六点中好点组的个数为________.(两点不计顺序)
)的图象C上.如果这六点中不同的两点的连线的中点仍在曲线C上,则称此两点为“好点组”,则上述六点中好点组的个数为________.(两点不计顺序)
11
分析:题干错误:x6-x1=5π,应该是:x6 -x1=5π,请给修改,谢谢.
由题意可得,只要研究函数y=sinx在[0,6π]上的情况即可.画出函数y=sinx在[0,6π]上的图象,数形结合可得结论.
解答:由于对称关系不因平移而改变,∴y=sinx与f(x)=sin(x+ )对称关系没有变.
)对称关系没有变.
根据函数的周期性,只要研究函数y=sinx在[0,6π]上的情况即可.
画出函数y=sinx在[0,6π]上的图象,如图所示:可得A1( ,0)、B1(
,0)、B1( ,0)、A2 (
,0)、A2 ( ,0)、B2(
,0)、B2(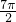 ,0)、
,0)、
A3 ( ,0)、B3(
,0)、B3( ,0).
,0).

由函数y=sinx的图象性质可得,“好点租”有:A1B1,B1A2,A2B2,B2B2,B2A3,A3B3,A1A3,B1B3,A1B2,A2B3,B1A3,
共11个,
故答案为 11.
点评:本题主要考查新定义“好点组”,正弦函数的图象的对称性的应用,函数y=Asin(ωx+∅)的图象变换规律,属于中档题.
分析:题干错误:x6-x1=5π,应该是:x6 -x1=5π,请给修改,谢谢.
由题意可得,只要研究函数y=sinx在[0,6π]上的情况即可.画出函数y=sinx在[0,6π]上的图象,数形结合可得结论.
解答:由于对称关系不因平移而改变,∴y=sinx与f(x)=sin(x+
 )对称关系没有变.
)对称关系没有变.根据函数的周期性,只要研究函数y=sinx在[0,6π]上的情况即可.
画出函数y=sinx在[0,6π]上的图象,如图所示:可得A1(
 ,0)、B1(
,0)、B1( ,0)、A2 (
,0)、A2 ( ,0)、B2(
,0)、B2(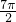 ,0)、
,0)、A3 (
 ,0)、B3(
,0)、B3( ,0).
,0).
由函数y=sinx的图象性质可得,“好点租”有:A1B1,B1A2,A2B2,B2B2,B2A3,A3B3,A1A3,B1B3,A1B2,A2B3,B1A3,
共11个,
故答案为 11.
点评:本题主要考查新定义“好点组”,正弦函数的图象的对称性的应用,函数y=Asin(ωx+∅)的图象变换规律,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )的图象C上.如果这六点中不同的两点的连线的中点仍在曲线C上,则称此两点为“好点组”,则上述六点中好点组的个数为 .(两点不计顺序)
)的图象C上.如果这六点中不同的两点的连线的中点仍在曲线C上,则称此两点为“好点组”,则上述六点中好点组的个数为 .(两点不计顺序)