题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求曲线在
,求曲线在![]() 点处的切线方程;
点处的切线方程;
(2)若曲线![]() 与直线
与直线![]() 只有一个交点,求实数
只有一个交点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求点![]() 处的切线方程,只要求出导数
处的切线方程,只要求出导数![]() ,则有切线方程为
,则有切线方程为![]() ;(2)曲线
;(2)曲线![]() 与直线
与直线![]() 只有一个交点,说明关于
只有一个交点,说明关于![]() 的方程
的方程![]() 只有一个实根,
只有一个实根,![]() 不可能是根,因此方程可转化为方程
不可能是根,因此方程可转化为方程![]() 只有一个实根,这样问题又转化为函数
只有一个实根,这样问题又转化为函数![]() 的图象与直线
的图象与直线![]() 只有一个交点,因此只要研究函数
只有一个交点,因此只要研究函数![]() 的单调性,极值,函数值变化情况,作出简图就可得出结论.
的单调性,极值,函数值变化情况,作出简图就可得出结论.
试题解析:(1)![]() ,
,![]() ,
,![]() ,所以切线方程为
,所以切线方程为![]() .
.
(2)曲线![]() 与直线
与直线![]() 只有一个交点,等价于关于
只有一个交点,等价于关于![]() 的方程
的方程![]() 只有一个实根.
只有一个实根.
显然![]() ,所以方程
,所以方程![]() 只有一个实根.
只有一个实根.
设函数![]() ,则
,则![]() .
.
设![]() ,
,![]() ,
,![]() 为增函数,又
为增函数,又![]() .
.
所以当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
所以![]() 在
在![]() 时取极小值
时取极小值![]() .
.
又当![]() 趋向于
趋向于![]() 时,
时,![]() 趋向于正无穷;
趋向于正无穷;
又当![]() 趋向于负无穷时,
趋向于负无穷时,![]() 趋向于负无穷;
趋向于负无穷;
又当![]() 趋向于正无穷时,
趋向于正无穷时,![]() 趋向于正无穷.所以
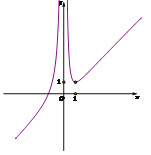
趋向于正无穷.所以![]() 图象大致如图所示:
图象大致如图所示:
所以方程![]() 只有一个实根时,实数
只有一个实根时,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目