题目内容
下列命题正确的是
- A.?x∈R,e|x|>||x|+1
- B.?x>0,|lnx|≤|x-1|
- C.?x∈(0,
 ),sinx=tanx
),sinx=tanx - D.?x∈(0,
 ),cos2x=1-
),cos2x=1-
D
分析:分别将x=0,x= ,代入e|x|>|x|+1,与|lnx|≤|x-1|比较大小后,可以判断A、B的真假;根据三角函数的性质,我们可以判断C的正误;从而得出正确选项.
,代入e|x|>|x|+1,与|lnx|≤|x-1|比较大小后,可以判断A、B的真假;根据三角函数的性质,我们可以判断C的正误;从而得出正确选项.
解答:∵当x=0时,e|x|=1,|x|+1=1,故A错误;
∵当x= 时,|lnx|=1,|x-1|<1,故B错误;
时,|lnx|=1,|x-1|<1,故B错误;
∵tanx=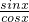 >sinx,故C错误;
>sinx,故C错误;
∴故正确命题只有:D
故选D.
点评:本题考查的知识点是全称命题与特称命题的真假判断,要判断一个全称命题是正确的需要严格的谁,而要说明其是错误的,只要举出一个反例即可;要判断一个特称命题是真命题,我们也可以只举一个适合条件的例子即可.
分析:分别将x=0,x=
 ,代入e|x|>|x|+1,与|lnx|≤|x-1|比较大小后,可以判断A、B的真假;根据三角函数的性质,我们可以判断C的正误;从而得出正确选项.
,代入e|x|>|x|+1,与|lnx|≤|x-1|比较大小后,可以判断A、B的真假;根据三角函数的性质,我们可以判断C的正误;从而得出正确选项.解答:∵当x=0时,e|x|=1,|x|+1=1,故A错误;
∵当x=
 时,|lnx|=1,|x-1|<1,故B错误;
时,|lnx|=1,|x-1|<1,故B错误;∵tanx=
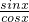 >sinx,故C错误;
>sinx,故C错误;∴故正确命题只有:D
故选D.
点评:本题考查的知识点是全称命题与特称命题的真假判断,要判断一个全称命题是正确的需要严格的谁,而要说明其是错误的,只要举出一个反例即可;要判断一个特称命题是真命题,我们也可以只举一个适合条件的例子即可.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
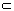 平面β,则下列命题正确的是
平面β,则下列命题正确的是  ,直线b
,直线b 直线a,b
直线a,b 平面
平面 ,则
,则
 则
则 B.若
B.若 , 则
, 则
 则
则 D.若
D.若